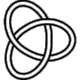
3_1
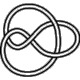
4_1
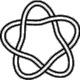
5_1
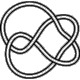
5_2
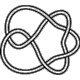
6_1
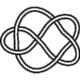
6_2
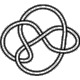
6_3
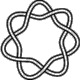
7_1
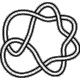
7_2
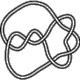
7_3
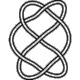
7_4
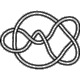
7_5
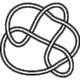
7_6

7_7
As part of work (see this, this and this.) on computing knotting probabilities Buks van Rensburg and I computed minimal knotted polygons on three cubic lattices: simple cubic, face-centred cubic and body-centred cubic. This adds to work done on the cubic lattice by Rob Scharein, Kai Ishihara, Javier Arsuaga, Yuanan Diao, Koya Shimokawa and Mariel Vazquez. After accumulating all this data I thought I would put it all in one place where it would be relatively easily accessible. Clicking on a knot below will take you to some minimal representations of that knot on these three lattices.
Buks hand-coded embeddings of the knots (up to 7 crossings) in the simple cubic lattice and then minimised them using the BFACF algorithm (see this for example). I coded up to 5 crossings by hand on the FCC and BCC and then minimised them using BFACF moves. After that I realised that I it was far easier to simply project Buks' simple cubic lattice embeddings into a sublattice of the FCC and BCC and then minimised them.
To find all the other embeddings (8 crossings and up) I used the minimal embeddings in the simple cubic lattice that appear in the paper by Scharein et. al. and then mapped them to sublattices of the FCC and BCC (simple perl scripts helped to automate the whole process). Finally the embeddings were minimised using the GAS algorithm (or a simple variant of it).
For way way more information on knots I strongly recommend taking a look atNote that the knot images below are taken from here.
I should really learn some php instead of having all these files. I'll get around to it.
Update February 27th 2011 - I have added the symmetry classes for all the knots with 7 crossings or fewer (corrected a couple of earlier errors). They are encoded as an oriented list of edges (and so have up to 48 symmetries). The edges are labelled as per here (in hexadecimal for the FCC). I have tentatively added the files for the 8 crossing knots - a few knots are missing a few classes, but I should have them patched in a week or so.
Update March 1st 2011 - I have fixed up the symmetry classes for all of the 8 crossing knots. Enjoy.
 3_1 |
 4_1 |
 5_1 |
 5_2 |
 6_1 |
 6_2 |
 6_3 |
 7_1 |
 7_2 |
 7_3 |
 7_4 |
 7_5 |
 7_6 |
 7_7 |
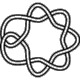 8_1 |
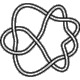 8_2 |
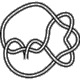 8_3 |
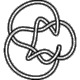 8_4 |
 8_5 |
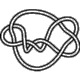 8_6 |
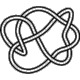 8_7 |
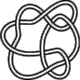 8_8 |
 8_9 |
 8_10 |
 8_11 |
 8_12 |
 8_13 |
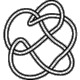 8_14 |
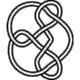 8_15 |
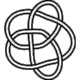 8_16 |
 8_17 |
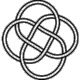 8_18 |
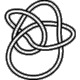 8_19 |
 8_20 |
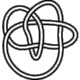 8_21 |