Math 300

Math 300, Section 101

Laurent Expansions and Singularities

Consider f(z)=1/(1-z). Below is a phase plot. Brightness corresponds with absolute value in this plot, that is why the pole at z=1 is white.

Here is the Taylor polynomial of this function up to order 3: it is 1+z+z²+z³. There are 3 zeros (black), and they are all on the unit circle (in fact, they are at i, -1, and -i). The unit circle is the circle of convergence.

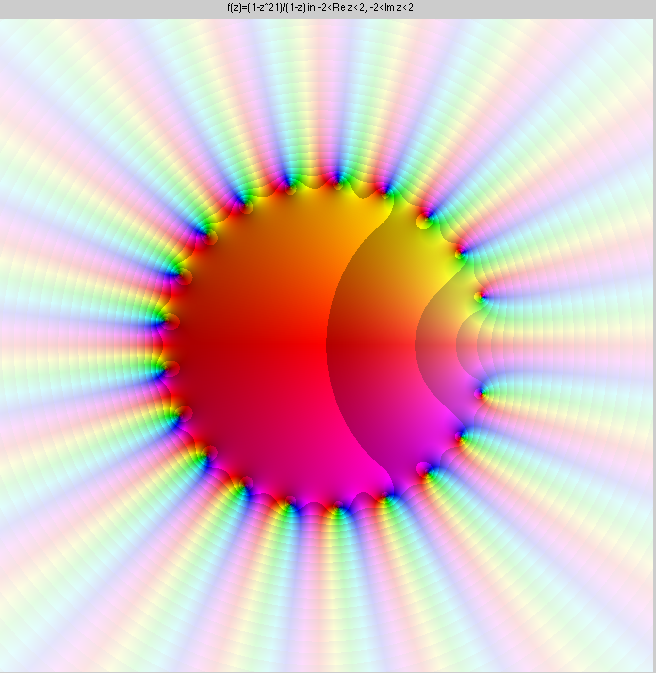
Here is the Taylor expansion up to order 20: 1+z+...+z²⁰. Notice how the interiour of the circle of convergence looks like the above plot of 1/(1-z), but the exteriour looks nothing like it.

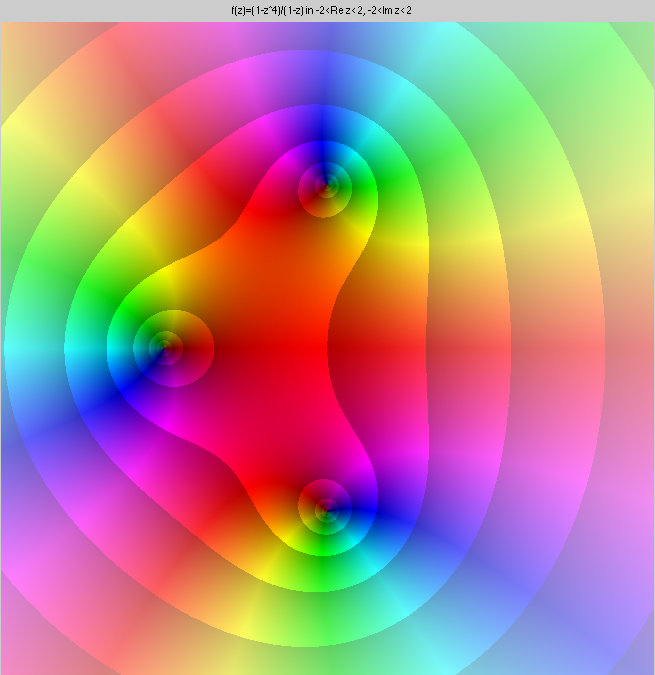
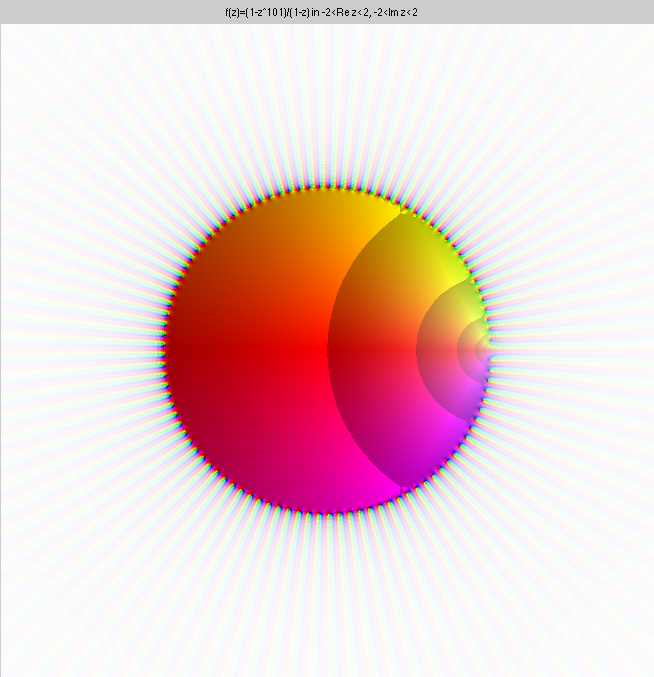
Finally, below are 100 iterations of the Taylor series. This is 1+z+...z¹⁰⁰. There are 100 zeroes (black) on the circle of convergence, but outside, the Taylor polynomial very quickly approaches ∞ (white). (The Taylor polynomial has a pole of order 100 at ∞.) Inside the circle of convergence, the Taylor series converges to the given function, outside, it converges to ∞ everywhere. On the circle of convergence it does anything it wants.

For comparison, here is the function f(z)=e^1/z,

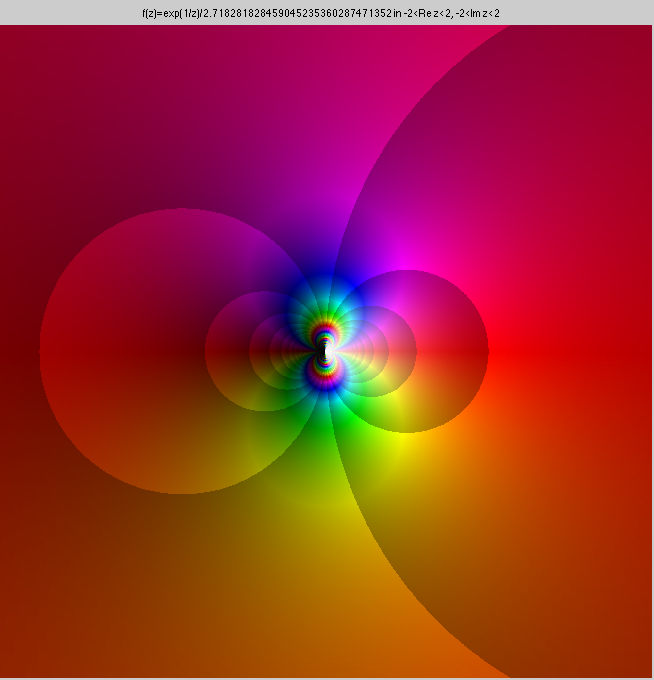
and its Taylor expansion up to order 20 at z=1. It doesn't look much different than the first example, even though this function has an essential singularity, rather than a simple pole on the circle of convergence. The 20 zeroes of the Taylor polynomial accumulate near the circle of convergence, although in this case, they are not exactly on it, they approach it from the outside, and get closer at every iteration.

Now, let's see some Laurent expansions. Consider the function f(z)=(z-1)^-1(z-2)^-1, which has simple poles at z=1, and z=2.

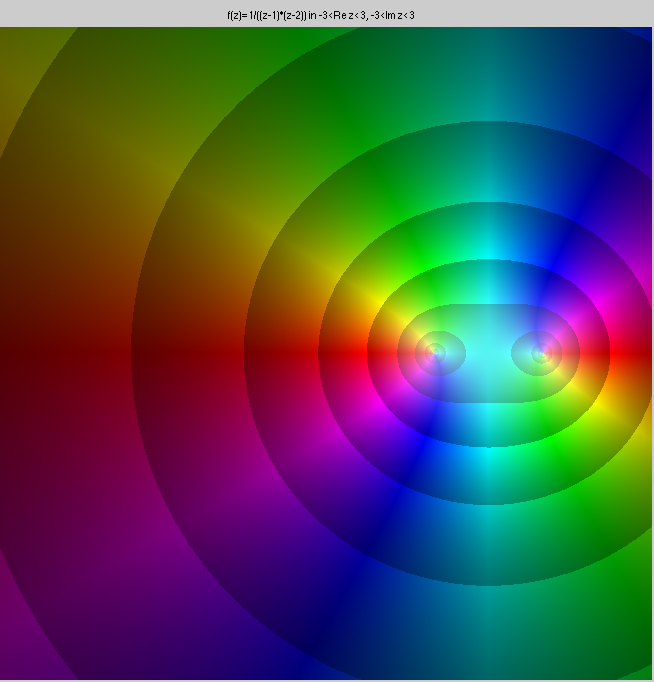
Here are three Laurent expansions centered at the origin, up to order 20, valid in a disk, an annulus, and the exteriour of a disk, respectively. In each case, the expansion converges to ∞ in the domains where it is not valid.

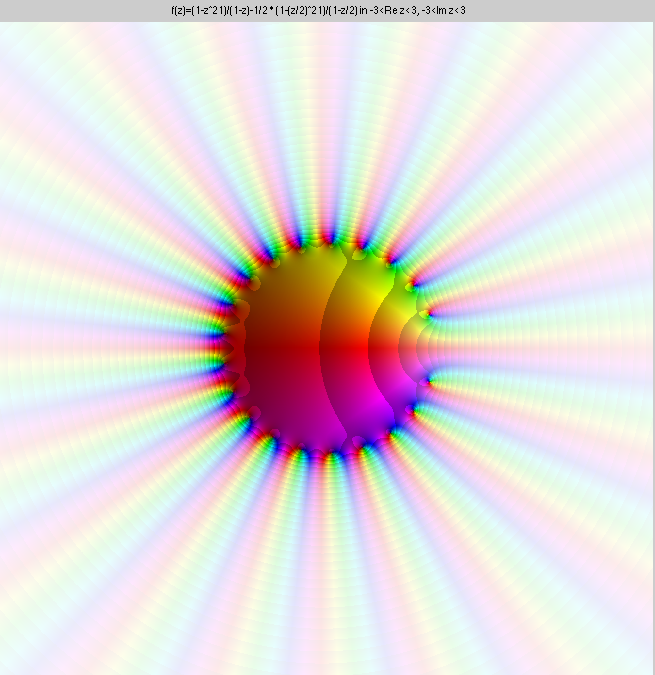
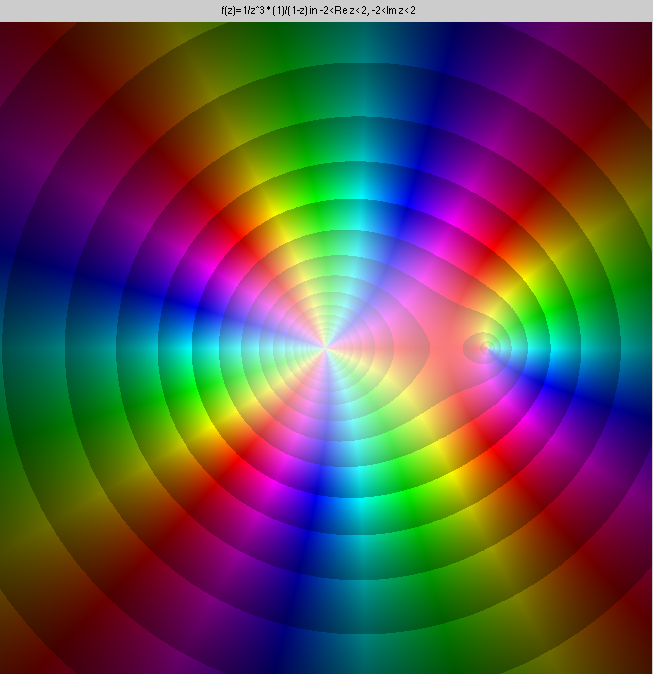
Here is the function f(z)=z^-3(1-z)^-1, which has a pole of order 3 at the origin, and its Laurent expansion up to order 20 in the punctured disk 0<|z|<1, and in the annulus 1<|z|<∞.

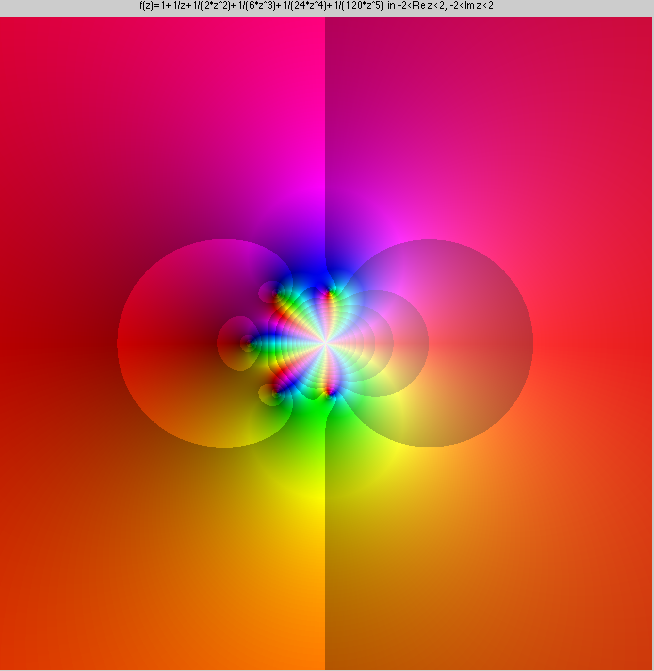
Here is the essential singularity e^1/z

And here are iterations up to order 3, 5 and 20 of the Laurent expansion at the origin, where the singularity is. Every one of these Laurent polynomials has a pole or order n at the origin, and n zeroes in a circle. This circle of zeroes gets closer and closer to the pole at the centre.

Here is the essential singularity e^1/z². We've zoomed in a bit, to see better. Remember: white corresponds to ∞, black to 0.

Here are a few more random pictures of essential singularities:

This is e^1/z²/z².

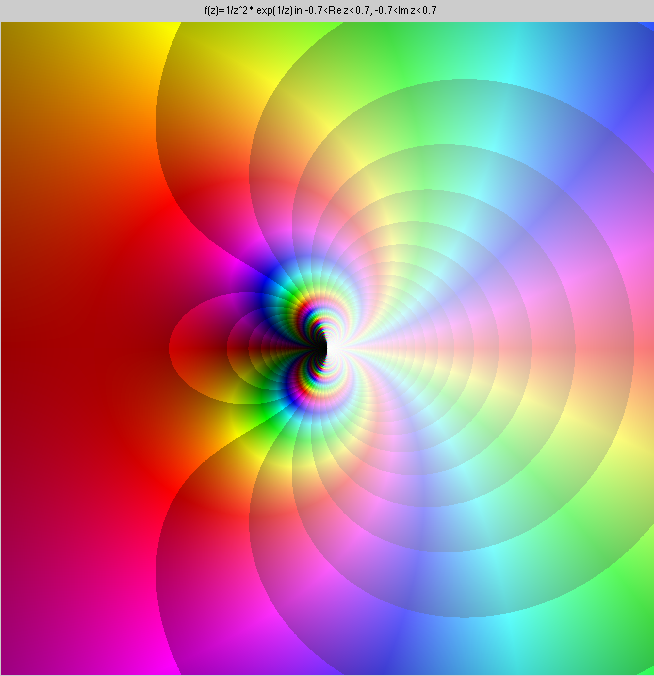
Here are three essential singularities:

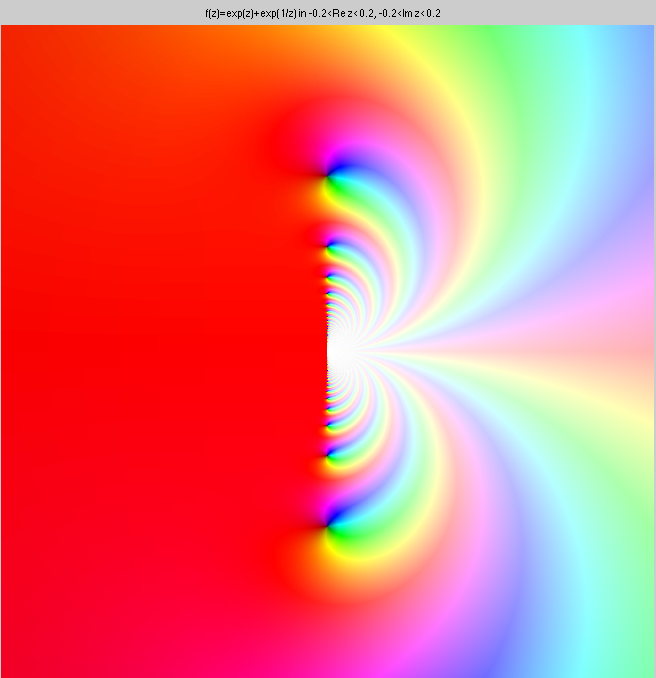
This is e^z+e^1/z. Note that there are infinitely many zeroes, and they accumulate at the origin. Still, this function is analytic everywhere except at the origin, so the singularity is isolated, and, of course, essential.

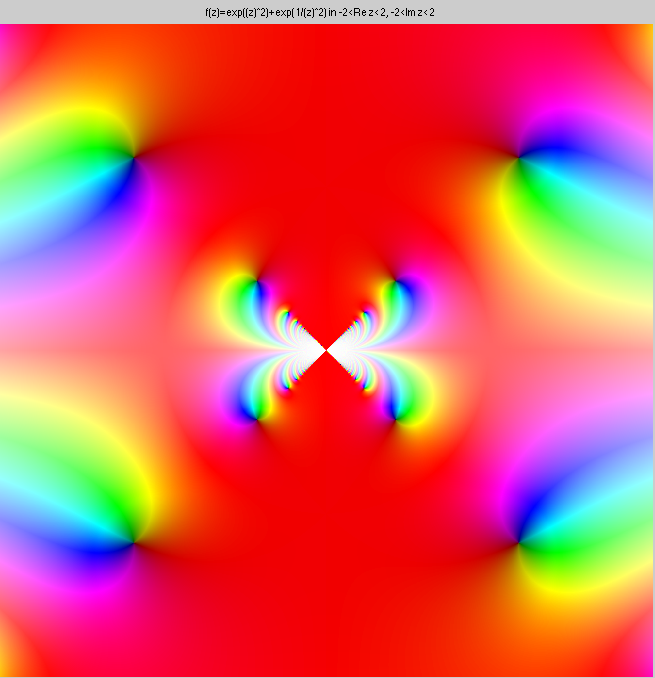
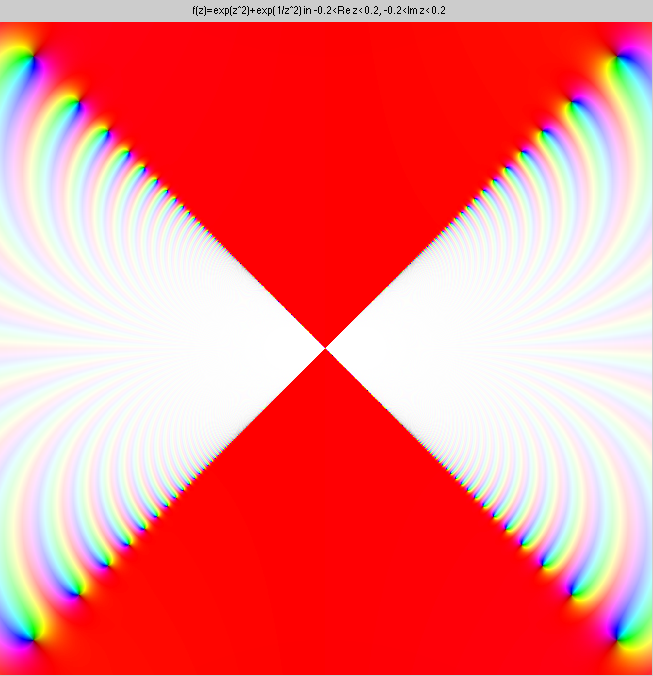
This is e^z²+e^1/z² at two different zoom settings

This is sin(1/z), with its isolated and essential singularity.

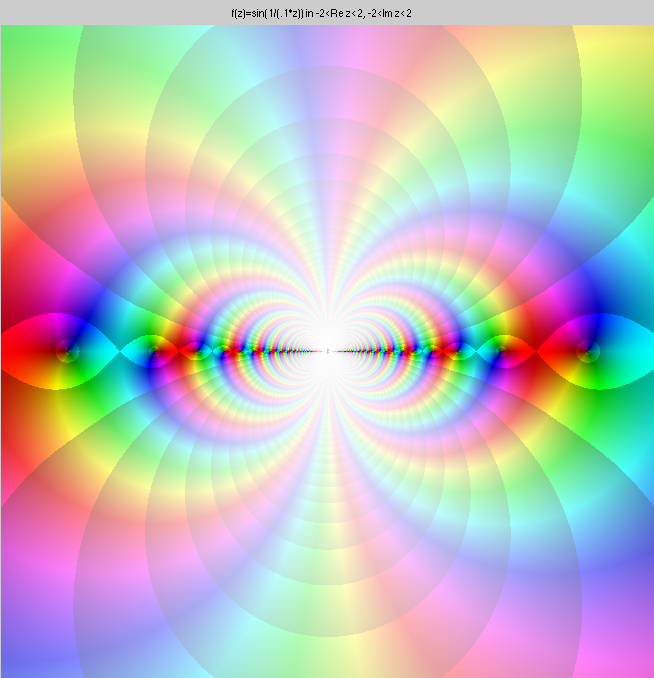
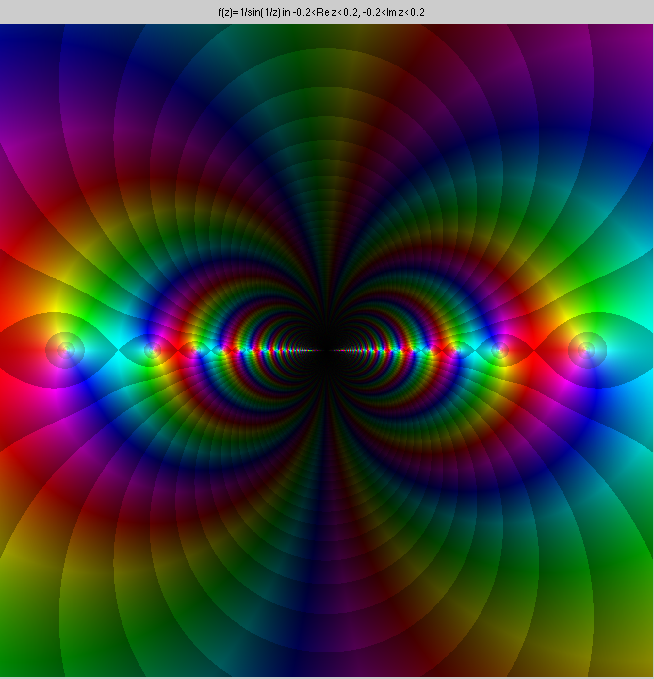
Finally two non-isolated singularities. The first is 1/sin(1/z). This does not look much different than sin(1/z). But because this time there are infinitely many poles accumulating at the origin, instead of infinitely many zeroes, the singularity at the origin is not isolated.

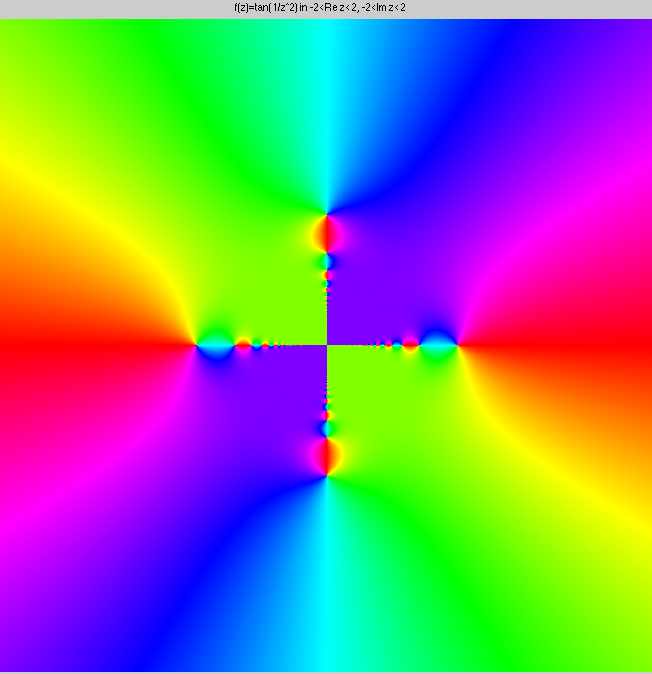
This is tan(1/z²). There are infinitely many poles and zeroes accumulating at the origin.

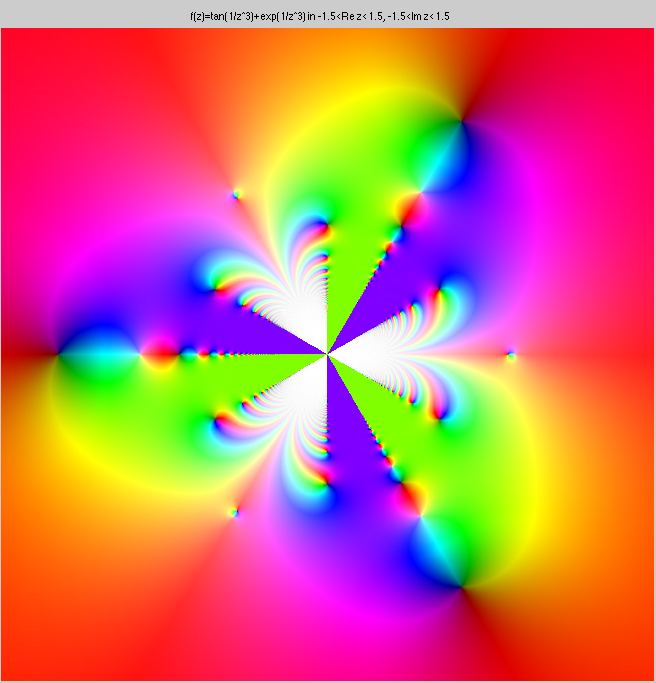
There is no limit to this silliness

back