"What is now proved was once only imagined."
-William Blake

Left: A rendition of a Calabi–Yau threefold, a six-dimensional space used in certain models of string theory.
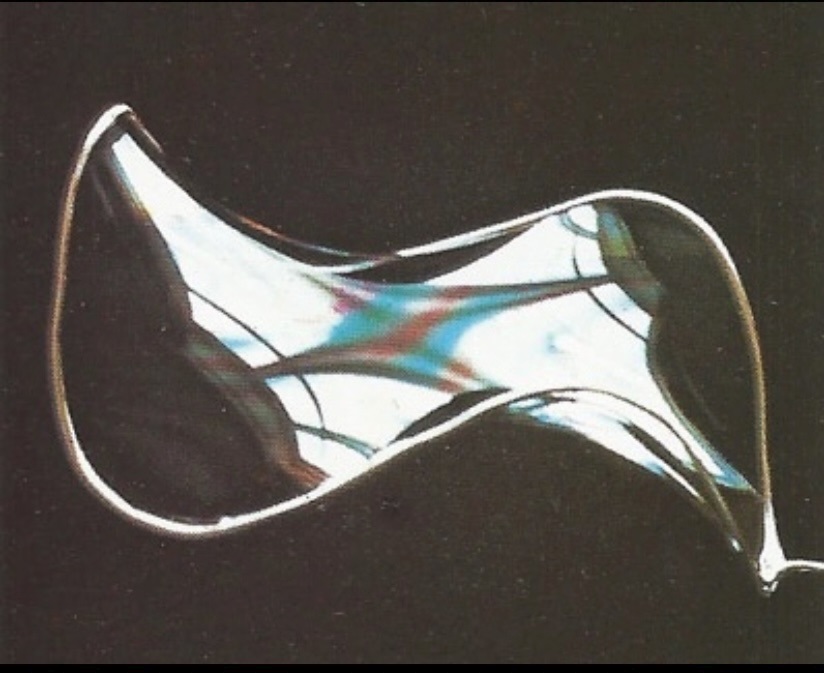
Right: A soap film will naturally produce a minimal surface, meaning that its area is critical with respect to normal variations of the surface.

My research is in geometric analysis, an exciting area at the intersection of differential geometry and partial differential equations, which finds many applications in theoretical physics as well as in other areas of math, including algebraic geometry and low-dimensional topology. My interests include geometric variational problems, such as

• existence and regularity of harmonic maps and minimal surfaces, and
• special Lagrangian submanifolds of a non-Kähler Calabi–Yau manifold.

While I was an undergraduate, I was researching matroids, which generalize the notion of linear independence in a vector space, affine independence in an affine space, and independence of edge sets in a graph.

Here is a list of my publications and preprints:

• Gromov–Hausdorff continuity of non-Kähler Calabi–Yau conifold transitions (with S. Picard and C. Suan)
  Preprint (2024) [arXiv]
• Girth conditions and Rota's basis conjecture (with S. McGuinness)
  Graphs Combin. 39, 51 (2023). [journal, arXiv]
• The Alon–Tarsi conjecture: A perspective on the main results (with S. McGuinness)
  Discrete Math. 342 #8 (2019), 2234-2253. [journal]
• Use of a varying turn-density coil (VTDC) to generate a constant gradient magnetic field and to demonstrate the magnetic force on a permanent magnet (with M. G. Abraham, M. Paetkau, S. R. Taylor, and C. M. Ross Friedman)
  Can. J. Phys. 91(3) (2013), 226-230. [journal]