Spherical Geometry:  
Exploring the World with Math
 



Ptolemy:  Picture courtesy of Almagest Ephemeris Calculator

 

Karen Franco
kffranco(at)interchange(dot)ubc(dot)ca
Student # 46347985
MATH 308, Section 102
Final Project

December 15, 2002

 


Table of Contents:

I.  Introduction

II.  The Basics of Spherical Geometry

III.  Great Circles

IV.  Spherical Triangles
    A Tale of Two Cities:  The Cross-Continental Application of the Solution of Spherical Triangles

V.  Conclusion

References

 


I.  Introduction

Captain Cook, mathematician?  It is a little known fact that Captain James Cook, discoverer of Australia, New Zealand, Papua New Guinea, Hawaii, Tahiti and other islands in the Pacific, was trained as both a navigator and as a mathematician.  In fact, mathematics and exploration have a long history dating back to the times of the Greek and Phoenician mariners.

In the modern world, mathematics is commonly regarded as a "sit-down" science -- a subject where problems are often solved while sitting down in a classroom or office, and applications often relate to theory, finance, or business.  However, during the days of exploration, when it was discovered that the world was indeed round and not flat, spherical geometry was integral in mapping out the world, in navigating the seven seas, and in using the position of stars to chart courses from one continent to another.

Spherical geometry is defined as "the study of figures on the surface of a sphere" (MathWorld), and is the three-dimensional, spherical analogue of Euclidean or planar geometry.  On a sphere, two lines can be parallel and still intersect each other not once but twice, the sum of the angles of a triangle is greater than 180°, and the shortest distance between two points on a sphere is along the perimeter of a great circle, which is not necessarily a straight line on a flattened map.  As the Earth's shape is roughly approximated by a sphere, these properties of spherical geometry aided explorers in charting out the globe and astronomers in plotting the course of planets and stars.  Present day applications of these same properties include planning flights, cruises, and satellite orbits around the world.    



II.  The Basics of Spherical Geometry

A sphere is defined as a closed surface in 3D formed by a set of points an equal distance R from the centre of the sphere, O.  The sphere's radius is the distance from the centre of the sphere to the sphere's surface, so based on the definition given above, the radius of the sphere = R.  

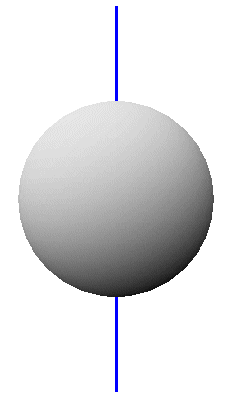An arbitrary straight line (not lying in the sphere) and sphere in three dimensional space can either (a) not intersect at all; (b) intersect at one point on the sphere, when the line is tangent to the sphere at the point of intersection; or (c) intersect at precisely two points, when the line passes through the sphere.  In this particular case, if the line passes through the centre of the sphere and intersects the sphere's surface in two points, the points of intersection form the antipodes of the sphere.  The North and South Poles (both the magnetic and geographic poles) are examples of antipodes on the globe.



 

Figure 1:  Line passing through the centre of the sphere; points of intersection are antipodes (PostScript file)

 

III.  Great Circles

Like lines and spheres, an arbitrary straight plane and sphere in three dimensional space can have (a) no intersection; (b) one point of intersection, when the plane is tangent to the sphere at that point; or (c) an infinite number of points of intersection, when the plane cuts through the sphere and forms a circle of intersection.  



Figure 2:  The meridians of longitude are examples of great circles (animated PostScript)

Great circles are defined as those circles of intersection which share the same radius R and same centre O as the sphere it intersects.  As their name implies, the great circles are the largest circles of intersection one can obtain by passing a straight plane through a sphere.  On the globe, a line or meridian of longitude forms half of a great circle running from pole to pole and with its centre at the centre of the Earth.  Another example of a great circle on the globe is the Equator, found at 0°  latitude.

Figure 3:  The parallels of latitude are examples of small circles  (animated PostScript)

Imagine a line from the North to the South Pole, passing through the centre of the globe.  The circles of intersection formed by the globe and a plane perpendicular to this imaginary line make up the globe's lines or parallels of latitude.  Each of these circles of intersection, with the exception of the Equator at which point the plane is at the midpoint of the pole-to-pole line, are called small circles precisely because their radii measure less than the Earth's radius R.

Navigators often used great circles to figure out the most efficient route to their destinations.  It turns out that the shortest path between two points on a sphere is along a great circle path, that is, along an arc of a great circle.  Have you ever wondered why a plane flying from Vancouver to the Philippines follows a route that takes you over Japan and Korea instead of flying a straight line over the Pacific Ocean?  Or why a flight from New York to Europe has to travel over the Maritimes and almost reach Greenland instead of making a beeline over the Atlantic Ocean?  The exact reason behind the logic of taking great circle paths to travel the world is explained and proved in the following section.



IV.  Spherical Triangles

When the arcs of three great circles intersect on the surface of a sphere, the lines enclose an area known as a spherical triangle.  Angles between great circles are measured by calculating the angle between the planes on which the great circles themselves lie.  How is this possible?  The spherical angle formed by two intersecting arcs of great circles is equal to the angle between the tangent lines formed when the great circle planes touch the circle at their common point (an antipode of the sphere since two great circles intersect each other in a line passing through the sphere's centre). 

Have you ever heard of a triangle whose angles sum up to greater than 180°?  In the figure below, the two meridians of longitude are separated by an angle of 90° and both lines of longitude fall perpendicular to the Equator (the only great circle of latitude).  Each angle in this particular spherical triangle equals 90°, and the sum of all three add up to 270°.

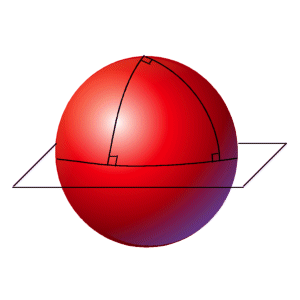
Figure 4:  In this triangle, the sum of the three angles exceeds 180° (and equals 270°)

Spheres have positive curvature (the surface curves outwards from the centre), hence the sum of the three angles of a triangle exceeds 180°.  On a plane with zero curvature, the sum of a triangles angles equals exactly 180°.

Like their angles, the length of the sides of a spherical triangle are measured in degrees or radians.  Specifically, the length of a side of a spherical triangle equals the measurement of its opposite angle.  In geography, the angle between two meridians of longitude equals the same number of degrees as the arc cut off by these lines of longitude on any circle of latitude.  So, in the above figure, each of the sides measures 90° since each of their opposing angles measures 90°.

The most useful application of spherical triangles and great circles is perhaps calculating the shortest-distance route between two points on the globe.  This application is often referred to as the solution of spherical triangles and makes extensive use of the well known Cosine Law for triangles on a plane:  c2 = a2 + b2 - 2ab cos C.  Given two sides of a spherical triangle and the angle between these sides, the solution for a spherical triangle yields the length of the third side.  
 

Figure 5:  The solution of a sphere
 

Figure 6:  The net of the tetrahedron used for the solution of a spherical triangle (animated PostScript)

Therefore the formula for the third side, a, of a spherical triangle, given two sides, b and c, and their included angle, A is

cos a = cos b · cos c + sin b · sin c · cos A
 


A Tale of Two Cities:  The Cross-Continental Application of the Solution of Spherical Triangles

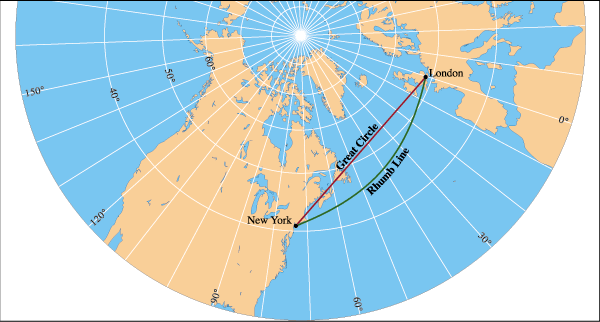
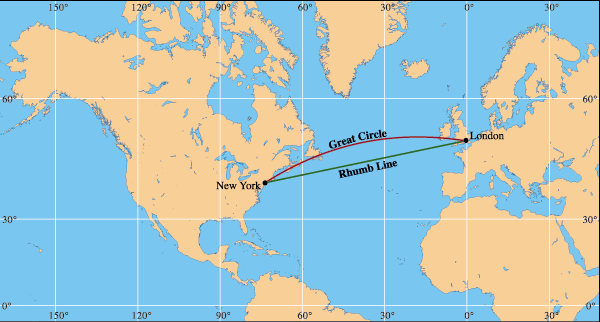
Figure 7:  Pictures courtesy of Maps.com

Imagine you had to find the best route from New York to London.  New York is geographically located at along the great circle of longitude 74° 0' W and approximately 40° 42' latitude north of the Equator, which makes it 90° - 40° 42' = 49° 18' south of the North Pole.  London, on the other hand, is located along the great circle of longitude 0° 5' W at approximately 51° 32' north of the Equator, which makes it 90° - 51° 32' = 38° 28' south of the North Pole.  The sides b and c are given by the length of the arcs from the North Pole to New York and London respectively, so b = 49° 18' and c = 38° 28'.  The angle A is given by the difference in meridians of longitude for the two cities:  A = 74° 0' W - 0° 5' W = 73° 55'.  

Applying the solution cos a = cos b · cos c + sin b · sin c · cos A, we get the following calculation:

cos a = cos 49° 18' · cos 38° 28' + sin 49° 18' · sin 38° 28' · cos 73° 55'
cos a = (0.6521 · 0.7830) + (0.7581 · 0.6221 · 0.2770)
cos a = 0.6412
a = 50.1186° or 50° 7'
 

This means that the great circle distance between New York and London is approximately 50° 7'.  In miles, given that one degree of a great circle is approximately 69 miles (110.4 kilometres), this distance measures approximately 50.1151° x 69 miles =  3458 miles (5533.0934 kilometres).


 
V.  Conclusion

Geometry derives its meaning from the Greek words geometria and geometrein which mean "measuring the earth".  Geography, on the other hand derives its meaning from the Greek words geographia and geographein which mean "describing or writing about the earth".  One would expect words so similar in meaning to be similar in concept as well.  However, the two fields were separate and distinct until the days of ancient Greece, when Ptolemy (astronomer, mathematician and geographer) made use of geometry in reasoning more about the earth and its shape:  

"In Geography one must contemplate the extent of the entire earth, as well as its shape, and its position under the heavens, in order that one may rightly state what are the peculiarities and proportions of the part with which one is dealing...  It is the great and exquisite accomplishment of mathematics to show all these things to human intelligence..."
 

Interestingly enough, it was also Ptolemy and not Christopher Columbus who discovered that the earth was spherical and not flat, and stated his rationale in the Almagest 1300 years before Columbus sailed around the world:  
 

"If the earth were flat from east to west, the stars would rise as soon for westerners as for orientals, which is false.  Also, if the earth were flat from north to south and vice versa, the stars which were always visible to anyone would continue to be so wherever he went, which is false.  But it seems flat to human sight because it is so extensive."  
 

Like geometry and geography, the worlds of spherical geometry (used in geography) and planar geometry (commonly taught in most geometry courses) are closely related and yet extremely different.  

Anybody who has completed high school level geometry (or to some extent, elementary geometry) knows that in Euclidean or planar geometry, two parallel lines never meet, the sum of the three angles of a triangle add up to 180°, and the shortest route to get from one point to another is a straight line.  In the world of spherical geometry, two parallel lines on great circles intersect twice, the sum of the three angles of a triangle on the sphere's surface exceed 180° due to positive curvature, and the shortest route to get from one point to another is not a straight line on a map but a line that follows the minor arc of a great circle.  Maps provide a way of translating the spherical view of the world to a planar view, by projecting the Earth's topologies and locations to a flattened surface using Hammer, Mercator or cylindrical methods.  A consistent and standard representation that minimizes projective distortions is yet to be established.

The discovery of spherical geometry not only changed the history and the face of mathematics and Euclid's geometry, but also changed the way humans viewed and charted the world.  Using this new knowledge, explorers and astronomers used the circular path of stars to navigate the earth to discover new lands and reason about the cosmos.

 


References:

Borowski, E.J. and Borwein, J.M.  Collins Reference Dictionary of Mathematics.  1989:  Collins.  London and Glasgow.

Casselman, Dr. W.  A Manual of Mathematical Illustration.  [MATH 308 text]

Hogben, Lancelot.  Mathematics for the Million.  1951:  W.W. Norton and Company, Inc.  New York.

Hogben, Lancelot.  Science for the Citizen.  1950:  W.W. Norton and Company, Inc.  New York.

Maps.com - Learn and Play.  Map Skills:  Great Circles.  [Maps.com web page]

Mariners' Museum, The.  The Mariners' Museum -- Newport News, Virginia.  [background image for web page, historical background]

Osserman, Robert.  Poetry of the Universe:  A Mathematical Exploration of the Cosmos.  1995:  Anchor Books, Doubleday.  New York.

Polking, John C.  The Geometry of the Sphere 1.  [basic information about spheres]

WhatIs?Com.  Latitude and Longitude:  a WhatIs Definition.  [what is latitude and longitude?]

Wolfram Research, Inc.  MathWorld:  Eric Weisstein's World of Mathematics.  [MathWorld web page]




TROUBLESHOOTING:

In order to run any of the PostScript files, you need a free PostScript interpreter installed on your computer:  GhostView and GhostScript are the most popular ones.  Click on the links to obtain these.

For latitude.ps and longitude.ps, make sure you have ps3d.inc in the same directory as these files (see KarenFrancoProject.zip file if this is missing).