Construction of a Pentagon on the cube Proof of Part I: Pentagon is Equilateral Proof of Part II: Pentagon is in One Plane Proof of Part III: Pentagon is Equiangular Proof of Part IV: Side of Dodec Form Apotome Construction of the Dodecahedron

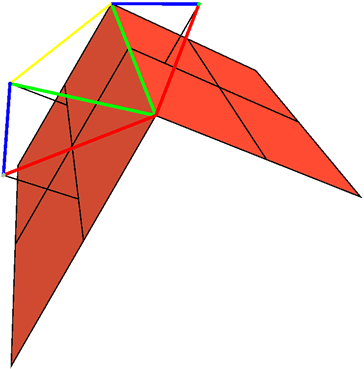
Since the magenta line equals the cyan, as shown in the green lines here. Similarly we can prove that the blue angle also equals the light green angle. Therefore the three angles equal one another. But if in an equilateral pentagon three angles equal one another, then the pentagon is equiangular, therefore the pentagon is equiangular. (Euclid XIII.7) And it was also proved equilateral, therefore the pentagon is equilateral and equiangular, and it is on one side of the cube. Therefore, if we make the same construction in the case of each of the twelve sides of the cube, a solid figure will be constructed which is contained by twelve equilateral and equiangular pentagons, and which is called a dodecahedron.

Back To Main Page