Euler’s Formula
V + F – E = 2
To view the following postscript files, please download ps3d.inc and place it in the same directory as the file you wish to view.
This project contains:
I.
Introduction
II.
The Definition of a Polyhedron
III.
Euler’s Own Proof
i.
Explanation
IV.
Legendre’s Proof Using Radial Projections
i.
Explanation
iii.
Difficulties
V.
A Proof Based Principally on Illustrations
i.
Explanation
ii.
Proof in Pictures
a.
Cube
b.
Dodecahedron
VI.
Conclusion
VII.
Bibliography
I.
Introduction
It is said that in 1750, Euler
derived the well known formula V + F – E = 2 to describe polyhedrons.[1] At
first glance, Euler’s formula seems fairly trivial. Edges, faces and vertices are considered by
most people to be the characteristic elements of polyhedron. Surprisingly however, concise labelling of
such characteristics was not presented until the 1700’s. Leonhard Euler, recognizing the deficiency,
began his investigation of general polyhedra, and the relationship between
their elements.
Euler emphasized five major
components of a polyhedron in an attempt to find the relationship between
them. These five components were
vertices, (a location where 2 or more edges meet), faces (contained and defined
by 3 or more edges), edges (defined as the “ridge or sharp edge”[2] of a
polyhedron), sides (used to refer to the sides of each face), and plane angles
(the angle found at a vertex, contained by 2 sides). These definitions, contrasted with the
features that
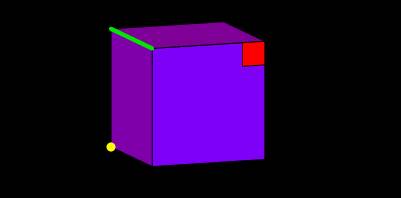
From above, green denotes the
edge of the cube; red denotes the plane angle;
the yellow sphere occurs at a
vertex; and all faces are shaded purple.
Sides are in black, they
surround the purple faces.
In the remainder,
let: - V be
the number of vertices,
-
F be the
number of faces,
-
E be the number
of edges,
-
S be the
number of sides, and
-
P be the
number of plane angles.
By naming each component, Euler
observed some general relationships that occur for all polyhedron. For example, the definition of a side leads
to the equation 2S = E, where S is the number of sides and E is the number of
edges. It can then be stated that the
number of edges must be an even number, for if this were not the case, it would
be possible to have a half of a side, which contradicts the definition of S.
By looking at the condition to form a
face, we can derive another formula.
Since a face is a surface enclosed by at least 3 sides, we can state
that S ≥ 3F. Furthermore, there
must be at least 3 faces surrounding every vertex ( F ≥ 3V ). Additionally, it can be stated that the
number of plane angles equals the number of sides, P = S, that 2E ≥ 3F,
and that 2E ≥ 3V
In summary: 2S
= E
S
≥ 3F
F
≥ 3V
P
= S
2E
≥ 3F
2E
≥ 3V
II.
The Definition of a Polyhedron
There are many definitions of a
polyhedron. The definition used in this
project given by P. Cromwell in his book entitled “Polyhedra” is the following:
“A polyhedron is the union of
a finite set of polygons such that
i.
Any pair of polygons
meet only at their sides or corners.
ii.
Each side of each
polygon meets exactly one other polygon along an edge.
iii.
It is possible to travel
from the interior of any polygon to the interior of another.
iv.
Let V be any vertex and
lef F1, F2, …, Fn be the n polygons which meet
at V. It is possible to travel over the
polygons Fi from one to any other without passing through V.”
III.
Euler’s Own Proof
i.
Explanation
Although Euler presented the formula,
he was unable to prove his result absolutely.
His proof is based on the principle that polyhedrons can be
truncated. Euler proceeds by starting
with a polyhedron consisting of a large number of vertices, faces, and
edges. By removing a vertex, you remove
at least 3 faces (while exposing a new face), and at least 3 edges. As you continue, more vertices are removed,
until eventually you will find that Euler’s proof degenerates into an object
that is not a polyhedron. A polyhedron
must consist of at least 4 vertices. If
there are less than 4 vertices present, a degenerate result will occur, and
Euler’s formula fails. While the proof
fails to prove his formula, it does show that truncated and augmented platonic
polyhedra satisfy the equation, (thereby including classes such as the
Archimedean solids, and pyramids).
ii.
Proof in Pictures
Click here to see
an example of Euler’s proof using an
octahedron.
IV.
Legendre’s Proof Using Radial Projections
i.
Explanation
Another interesting proof [3] that
has wider applications, is a proof credited to Adrien Marie Legendre. This proof inscribes a convex polyhedron
inside a sphere, where the centre is found in the region enclosed by the
polyhedron, and the polyhedron is fully inscribed. We then proceed to project light rays from
the origin through each of the vertices on the polyhedron. By finding where these rays intersect the
sphere, and connecting the points of intersection by the arcs that characterize
the shortest distance between two points along the sphere, we produce a radial
projection of the polyhedron. Vertices
are now the points where the arcs meet, edges are now arcs, and faces are now
spherical polygons. By combining the
characteristics of a sphere, spherical polygons, and the summarized characteristics
of vertices, edges, and faces (from above), Euler’s formula can be
derived.
Main facts:
-
If you sum all of the angles surrounding a vertex, the resulting angle
will be 2π. It follows that the
total angle sum around all the vertices will be 2πV.
- From above,
2S = E.
- Each side
has an angle of π.
- Each face
has an angle of 2π.
- The surface
area of a sphere of R=1 is 4 π.
Let’s now establish the equation for the
surface area of a sphere. Let us assume
the radius of the sphere is 1.
Area of a Spherical Polygon** = angle sum – sides on single face (π) + 2π
Surface Area = (# of spherical polygons mapped on the sphere) (Area of Spherical Polygon)
Surface Area = V( angle sum) - Sπ + 2πF
4 π = 2 πV – 2E π + 2πF
If we divide both sides of the equation by 2π,
we get the formula:
2 = V – E + F
ڤ
**This
formula is from Girard’s Theorem for spherical polygons, although no further
discussion of this theorem is provided in this project.
ii.
Proof in Pictures
The following demonstrates elements of
Legendre’s proof of Euler’s formula through pictures, by inscribing a
tetrahedron inside a unit sphere. Click here to view it.
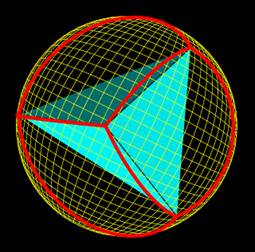
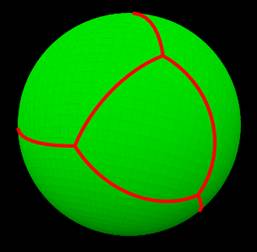
iii.
Difficulties
At first glance, it seemed like an easy
task to solve for the path along the surface of a sphere that connected two
points. However, upon attempting to code
such a procedure, it turns out there are some interesting questions that need
to be answered.
Let us first look at how to parameterize a
unit sphere of form x2 + y2 + z2 = 1. Let u, v be the parameters we introduce to
describe this curve. This being said,
any point on the sphere satisfies the equation
( cos(u)cos(v)
, cos(v)sin(u), sin(v) ) where 0o
≤ u, v ≤ 360o.
However, knowing how to parameterize the
unit sphere is unnecessary when trying to derive the direct path from any two
points, A and B, because there is an additional condition that must be
satisfied. To find the appropriate arc,
we must find the plane that contains A, B, and the origin of the sphere. This plane will also contain all of the
points that describe the path between the two points.
After looking at different cases, I found
the easiest way to find the arc along the great circle was to calculate the
midpoint between the two points we wish to connect. Let C be the centre of the sphere.
Let A = (xA, yA, zA),
B = (xB, yB, zB), and C = (0, 0, 0).
The direction of the midpoint is therefore M, where
M = [ ((xA+ xB)/2),
((yA+ yB)/2), ((zA+
zB)/2) ].
To find the midpoint along the arc of the
great circle, we must therefore find where the vector of the midpoint
intersects x2 + y2 + z2 = 1.
To do accomplish this, you can find the unit length
M, and divide M by it. This will result
in the midpoint. Therefore, the midpoint
along a great arc, m, is:
m = M / ||M||
V.
A Proof Based Principally on Illustrations
i.
Explanation
I found Von Staudt’s proof to be one of
the nicer proofs for Euler’s formula.
Von Staudt’s proof begins by picking any vertex on a convex
polyhedron. From this vertex, we look for
a vertex that has never been coloured, and connect the vertices by colouring
along the edge that connects them. Now
at the new vertex, we look for another vertex that has never been
coloured. If we find one, we connect the
vertices and colour along the edge that connects them again. We proceed in this fashion until there are no
more vertices to be visited.
If there are no more vertices to colour,
then all vertices have been coloured.
When traversing a polyhedron in this manner, we can see that this proof
requires that there is always a path that touches all vertices only once.
Around the same time that this proof was being published, an Irish
mathematician Sir William Rowan Hamilton (1805 – 1865) was examining the
problem of finding a path in a graph, or along a solid, where each vertex is
traversed only once. This path is called
a Hamiltonian circuit, and finding whether or not a circuit exists in a figure
is quite a challenge. To solve the
problem on an arbitrary graph is known to be intractable; no efficient
algorithm is known. Hamilton actually
created this idea as a sort of puzzle, find the path to connect every vertex on
a dodecahedron, visiting every vertex only once, and sold his dodecahedron
puzzle to an Irish merchant who began to sell it. It turns out that it is quite a difficult
task to identify whether or not a solid has a Hamiltonian circuit or not, and
it may require a proof by exhaustion to determine whether or not a path is
possible. However, it has been proven
that all Platonic solids, Archimedean solids, and planar-4-connected graphs
have Hamiltonian circuits.[4]
As we begin our proof [5], we
initially connect 2 vertices, and for every other edge we shade (let’s use
red), we find another vertex that we previously had not visited. Therefore, by counting the number of edges
that we shade red we can determine the number of vertices. The formula is:
Red Edges = V – 1
Furthermore, Von Staudt states that all
the vertices have been coloured. To
prove this, assume this is not the case.
Then there would be a vertex that is not coloured, which means we were
not done colouring our edges red.
Next we will begin by examining
faces. Pick a face and shade it green,
as well as any edges that have not yet been coloured red. Proceed by finding another face who has only
one green side, and shade green as before.
Continue until there are either no more faces to colour that satisfy the
condition. Since it is impossible that a
face exists with all four sides coloured, all faces must be shaded green. The relationship between green edges and
faces can be described as:
Green Edges = F – 1
The total number of edges, E, will equal
the number of green edges and red edges.
E = Red Edges + Green Edges
E = V – 1 + F – 1
Therefore,
E = V + F – 2
i.
Proof in Pictures
I have illustrated Von Staudt’s proof for a cube
initially to clearly demonstrate how the proof is to proceed. Next, the same proof is illustrated on a dodecahedron.
VI.
Conclusion
For over two centuries people have
discussed, proven and disproved Euler’s formula. The sample proofs I have provided by no means
represent the sole representations of Euler’s formula. It is possible to find proofs based on
electrical charge that will prove the formula.
There are others that use
VII.
Bibliography
1.
Casselman,
Bill, A Manual of Mathematical Illustration, http://www.math.ubc.ca/~cass/graphics/text/www/
2.
Cromwell,
Peter, Polyhedra,
3.
Dr.
Math, Regular Polyhedra, http://mathforum.org/dr.math/faq/formulas/faq.polyhedron.html#icosahedron
4.
Geometry
Junkyard, 17 Proofs of Euler’s Formula, http://www.ics.uci.edu/~eppstein/junkyard/euler/
5.
Polking, John C., The Geometry of a sphere,
http://math.rice.edu/~pcmi/sphere/gos6.html
6.
7.
Wolfram
Research, Hamiltionian Circuit, http://mathworld.wolfram.com/HamiltonianCircuit.html
8.
Wolfram
Research, Polyhedron, http://mathworld.wolfram.com/Polyhedron.html