One way of calculating the volume: the octahedron can be divided into 20 tetrahedra.
Each can be calculated using the pyramid method.
To get the vertices, take a look at this picture:
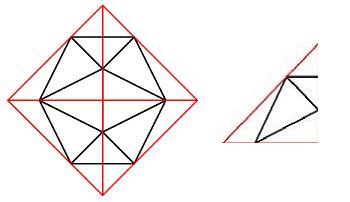
Each vertex of the icosahedron lies on the edge of octahedron,
is divided into 2 lines with the golden mean ratio Ø.
Another way to calculate the volume is divide the icosahedron into 3 parts.
The top part: 
The angle between the two red lines on the pentagon is 360/5=72°.
Let r = radius of the pentagon, a = length of edge, by the cosine law:
a² = r² + r ² - 2r²cos(72°)
The height of the pyramid is calculated by the Pythagoras theorem. h² = r² + a².
The bottom part of the icosahedron is the same.
The top view of the middle piece: 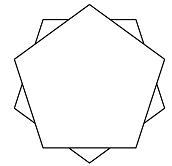
V = [5 × (3 + √5) / 12]a³
|