| Properties of the Octahedron |
| Faces: 8 trianglesVertices: 6, each with 4 edges meeting
Edges: 12Dihedral angle: 109°28' |
| The Symmetry |
 |
| Surface Area |
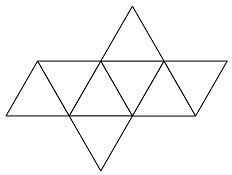
Let r = the distance from center to one vertex.
The length (a) of edge, by the Pythagoras Theorem, = r√2.
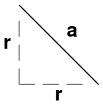
Then the area of one triangle is (a × h) / 2, where h = √[a² - (a/2)²].
And the area of the octahedron is 8 × the area of one triangle.
|
| Volume |
The octahedron can be divided into two pyramids.
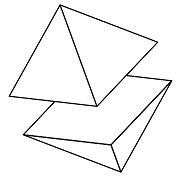
The volume of one pyramid = (base area × height) /3. In the case of the regular octahedron,
the base area = a².
And so, the volume of the octahedron = 2 × the volume of pyramid.
V = (√2 / 3)a³ |