OCTAHEDRON



See the octahedron rotating around the x, y, z axis.
Properties of the Octahedron
  • Faces: 8 triangles
  • Vertices: 6, each with 4 edges meeting
  • Edges: 12
  • Dihedral angle: 109°28'
    • The Symmetry
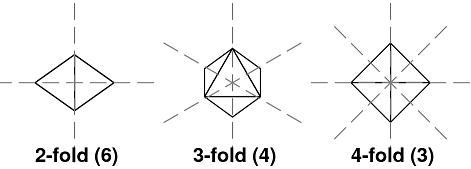    Surface Area

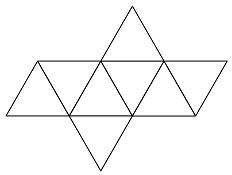
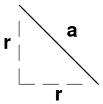
    Let r = the distance from center to one vertex.
    The length (a) of edge, by the Pythagoras Theorem, = r√2.

    Then the area of one triangle is (a × h) / 2, where h = √[a² - (a/2)²].
    And the area of the octahedron is 8 × the area of one triangle.
    Volume
    The octahedron can be divided into two pyramids.

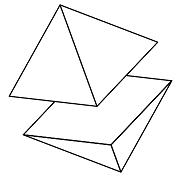
    The volume of one pyramid = (base area × height) /3. In the case of the regular octahedron, the base area = a².
    And so, the volume of the octahedron = 2 × the volume of pyramid.
    V = (√2 / 3)a³