René Descartes (1596-1650) set the foundation of analytic geometry with his well-known work La géométrie. La géométrie is the earliest book in which the notation is not so different from our own. Descartes was the first mathematician to write ab as a symbol of a times b. He was also the first one to use x and y in the coordinate system, although in a different order. He used x for the vertical axis and y for the horizontal axis. His contemporaries found his work difficult to follow since he choose to omit many things in order to leave the reader with some things to discover on their own.
I have taken one of his proofs from La géométrie and filled in some of the gaps and expressed it using more pictures. The proof is a construction that he uses in order to classify a curve within a specific class. He called all the conic sections the first class, meaning the equations with a highest degree of two. The second class belonged to the curves with equations containing terms with a third or fourth degree. His method, comparing the curve to a line using a ruler and some triangles, is able to find the equation and thereby classify the curve.
We want to know what degree this curve is.

 
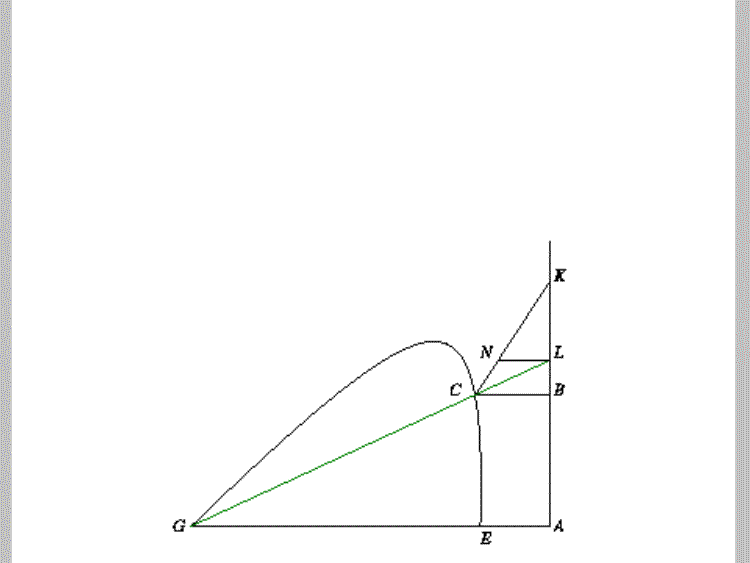
This was the picture originally shown in La géométrie. Choose an arbitrary straight line KA and fix the ruler (green) at G and place it at an arbitrary point L.
 

The same equation will result using any point L. To see a slide show of this, click on the link below. You need ghostview to open this.

slide_show.ps

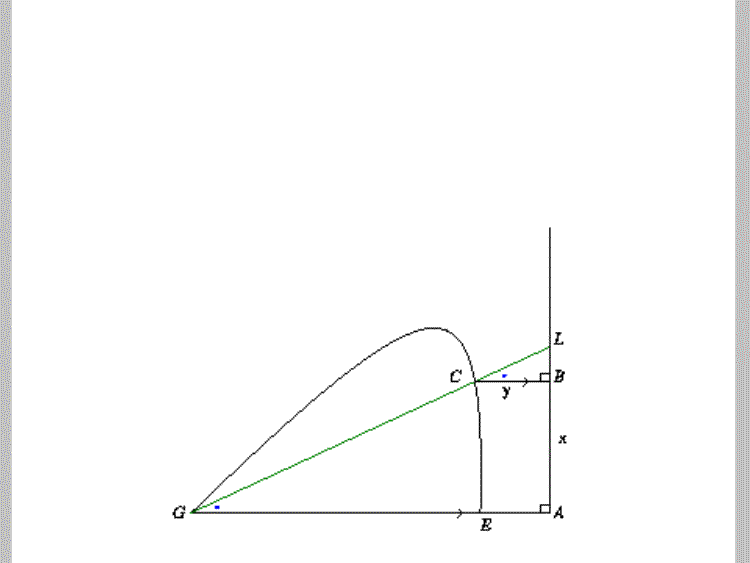
First, fix the ruler at the point L. Then construct a line parallel to GA at the point C. This creates the line CB with a length of y.
Now, connect C and K and construct NL to be parallel to CB and GA.
Zooming in on triangle CBK, we can see that triangle CBK is similar to triangle NLK since all three angles are equal. Thus, all the sides are proportional. So c/b = y/BK, making BK = yb/c
 

To see a proof on similar triangles, click on the link below. This proof is by David Hilbert (1862-1943). Again, you need ghostview to open it.

simtri.ps

Therefore, BL = yb/c - b
BK = yb/c
BL = yb/c - b
AK = x + yb/c - b
Triangle GAL is similar to triangle CBL since all three angles are equal.

 
y/(yb/c - b) = a/(x + yb/c - b)
y(x + yb/c - b) = a(yb/c - b)
yx + y2b/c - yb = yab/c -ab
y2b/c = yab/c - ab + yb - yx
y2 = ya - ac + yc - yxc/b
Since the highest degree is two, this curve is a conic section. In fact, it is a hyperbola.
 

Now that we know it's a hyperbola, the next problem that we want to address are the asymptotes.
Descartes ended his proof here without addressing this problem.
This next construction and proof is by Van Schooten.
From the slide show, we saw that EA = NL. Thus, EA = c and GA = a.
Extend AG to make a point D with DG = EA.
Then DG = NL = c.
Draw DF parallel to KC.
Claim: DF and AF are the asymptotes to the hyperbola GCE.
Proof: Extend BC to intersect DF at I.
Draw DH parallel to AF intersecting BC at H.
Triangle NKL is similar to triangle IDH since all three angles are equal.
Thus, KL/LN = DH/HI
DH = AB = x, KL = b, and LN = c.
Therefore b/c = x/HI, so HI = cx/b
Since HB = DA, HB = c + a
Therefore IB = a + c - cx/b and IC = a + c - cx/b - y
(IC)(BC) = (DE)(EA), a property of a hyperbola with respect to the distances between it and its asymptotes.
Thus, (a + c - cx/b - y)y = ac
or y2 = cy - cxy/b + ay - ac, which is the same equation as before.
Therefore, AF and DF are the asymptotes to the hyperbola GCE.
Q.E.D.