Kelvin Wave Pattern

When we look at ducks, boats, ships and other objects moving through calm water we can see that they produce a characteristic surface pattern.  The envelope of these waves stands at a fixed angle of 19.5 degrees and the wake has a characteristic feathered pattern.  These patterns are named after Lord Kelvin (William Thomson). This project will examine the math behind pretty pictures and model the pattern using postscript. 

In the moving object or moving pressure point problem, we need to use the Fourier or Laplace transform method to help us find a solution. The boundary value problem for the moving pressure point can be formulated as follows:

Fxx + Fyy + Fzz = 0   

where: Fxx +Fy = 0   at   y = 0, x and z cannot = 0

and F is finite as y approaches infinity.

We want to look for some parametric equations for x and z which we can plot to get a picture of our Kelvin Wave Pattern. 

We can find these parametric equations by solving the boundary value problem above:

x= -Y(2cos t - cos³ t)= -(1/4) Y(5cos t - cos 3t)

y= -Y(cos² t sin t)= -(1/4) Y (sin t + sin 3t)

Here Y is the phase of the wave. If we make Y = 1, we can produce the characteristic Kelvin Wave pattern. 

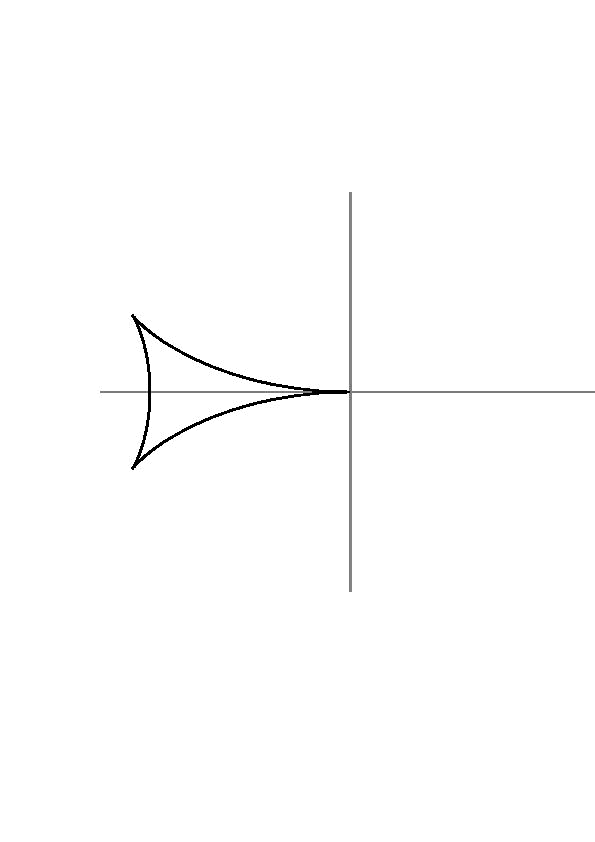
The characteristic angle 19.5 degrees comes from the cusps which lie at x= -Y(4/9)( sqrt 6) and z= -Y(2/9)(sqrt 3). The value of tan-1  (sqrt 3)(sqrt 6)(1/2) is 19.47 degrees.

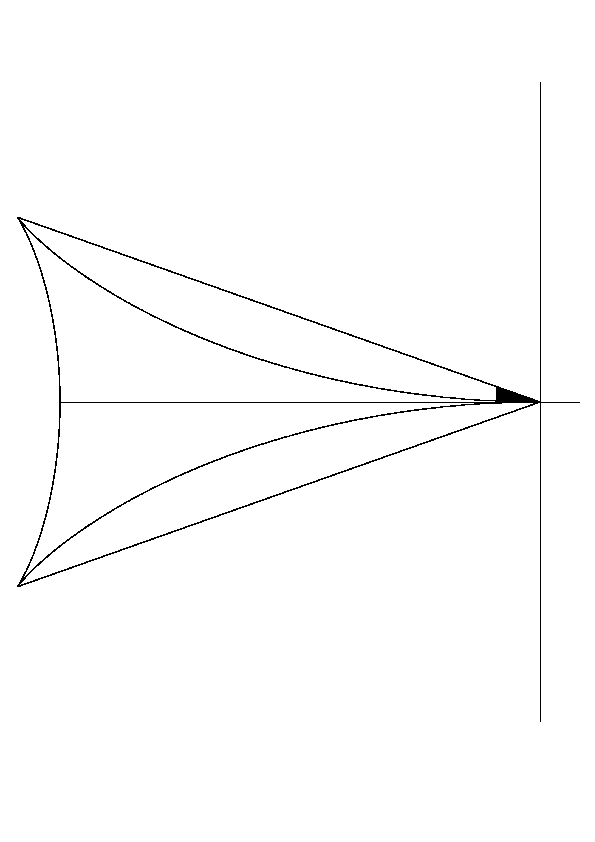
Plotting many different values of Y, we begin to get the wake that we saw behind the boat and the duck. 

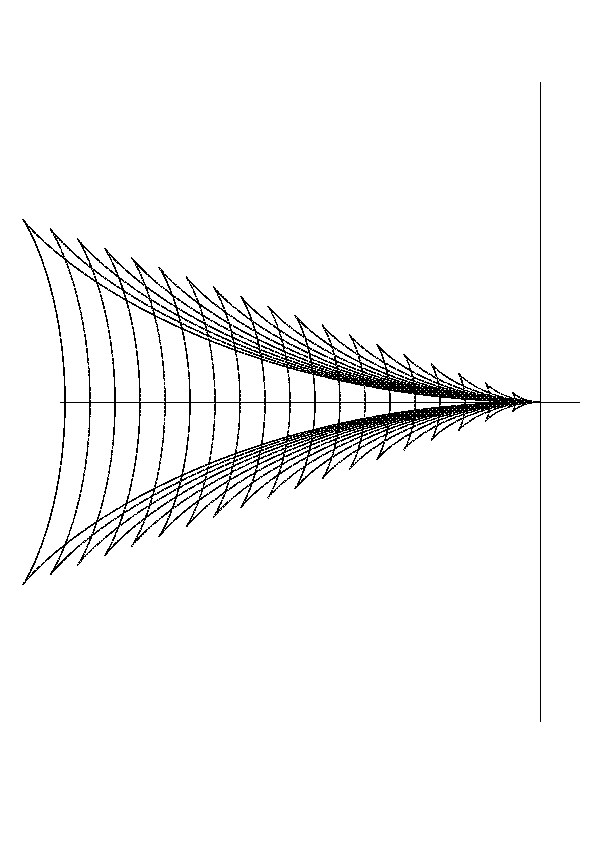
If we plot many phases and use colors to symbolize the height to the wave we can see that these equations work very well. The little yellow ellipse is a boat and the blue and black pattern is the surface of the wave. 

Math 309 Project Carmen Lazzarotto