Earlier, when we studied Snell's Law, we spoke of dispersion, where refraction depends on the wavelength of light being refracted. Chromatic aberration is the problem of different colours of light being focussed at different points along the optical axis.
In our treatment of the axioms of optics, we listed refractive indices for glass depending on wavelength.
| nglass as a Function of Wavelength | ||
|---|---|---|
| Wavelength, nm | Colour | nglass |
| 434 | blue | 1.528 |
| 486 | blue-green | 1.523 |
| 589 | yellow | 1.517 |
| 656 | orange | 1.514 |
| 768 | red | 1.511 |
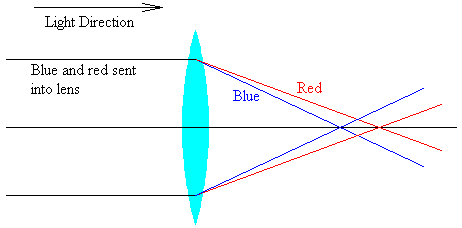
In essence, blue light is bent more than red light.
For a typical converging lens, these values result in a picture like the following.

Chromatic aberration is remedied in much the same way as spherical aberration; two lenses are joined together so that their aberrations cancel each other.
Unfortunately, chromatic aberration is very difficult to remove. Configuring a lens system so that blue and red light focusses at the same point does not guarantee that orange and green light will focus at the same point, and so on. Generally, lens designers aim to correct the aberration for a certain pair of colours (whichever colours are most important for the particular application of the lens system). The resulting correction is generally good enough so that any residual chromatic aberration for other colours in the visible spectrum are negligible.