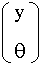
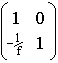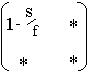Math 309 Final Project
| Look at this world through transform matrix | |
|---|---|
|
To all viewers, This page is aimed to illustrate some phenomenons that we "see" in the perspectives of mathematics. Mainly, we would focus on astigmatism, pincushion and barrel distortion, as well as chromatic abberation. All these topics are very interesting to me, since they are always hanging around in our daily life. For example, it is easy to find astigmatism on some senior people. Maybe we would also suffer it later in our life. However, with the explanation of transformation matrix, we would learn more on how to tackle or correct it. Hope you enjoy this page!
- Joseph Ho
|
What's Transform Matrix?
Transform matrix consists of three types of matrix. They are (i)translation matrix, (ii)refraction matrix and (iii)reflection matrix. Multiplication of any combination among them would result a transform matrix which follows the progress of a ray through any optical system.
How can Astigmatism be corrected?
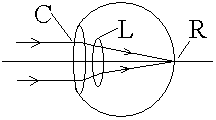
But, how's it related to mathematics? By transform matrix, we can understand and control the path of light. Cornea is a kind of lens made by human tissue. Astigmatism can then be illustrated from the point of view of mathematics, and further described by transform matrix. Moreover, It also provides the requierd data to produce correctness lens and even refractive surgery. Details... What's Barrel and Pincushion distortion?
What's Chromatic Aberration?
|
| Transform Matrix |
|---|
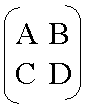
Transforam matrix is also known as an ABCD matrix. Since it is a set of 2X2 matrix with A starts from the top left hand corner and B, C, D filled in it in a clockwise direction. A, B, C and D can be any real number, but the determinant of the matrix is always 1.
Translation matrix usually represents the ray pass through a media without changing angle. In other words, the ray is a straight line without bending within a media. Such ray tracing could be expressed by matrix with B equals the distance (S) the ray passed through in that media divided by the index of refraction (n) of that media. For instance, a ray passing through the air over 2 cm has B = 2 as refractive index of air is 1. In this case, all the values are unified by 'cm' in the matrix. (B = s/n)
Refraction matrix usually represents the ray pass through lens surface, in which the ray bends with respect to the index of refraction of the lens. Thus, C in the rafraction matrix will become -(n2-n1)/R. If the light ray comes from the left of the lens, n2 and n1 would be the index of refraction on the right media and the left media of the lens respectively. R is the radius of the lens, it has a negative value if the lens bend backward (with centre to the left of the surface). Reflection matrix represents the ray reflected usually by a mirror. This matrix is very similar to refraction matrix but involved only one media, resulting C = 2n/R. R is the radius of the mirror. |
| Correction for Astigmatism |
|---|
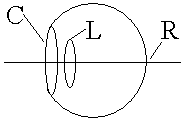
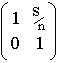
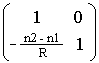
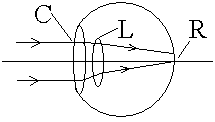
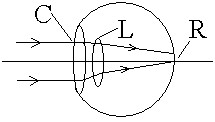
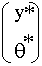 =
=