
Early physicists such as Issac Newton and Christiann Huygens thought tt was a steady stream of particles and had a wave motion. Indeed, such theories were correct but were unproven because light does indeed consists of moving quantas of photons which are packets of particles of pure energy. It was not until 1802, that Thomas Young proved that light does have a wave motion. In his experiment, he hypothesized that parallel beams of light should produce a brighter area where they overlapped if light were a steady stream. Instead, they produced bright bands separated by dark bands, the result of two sets of waves coinciding or canceling each other out. Thus, light is a form of wave.
|
 |
|
|
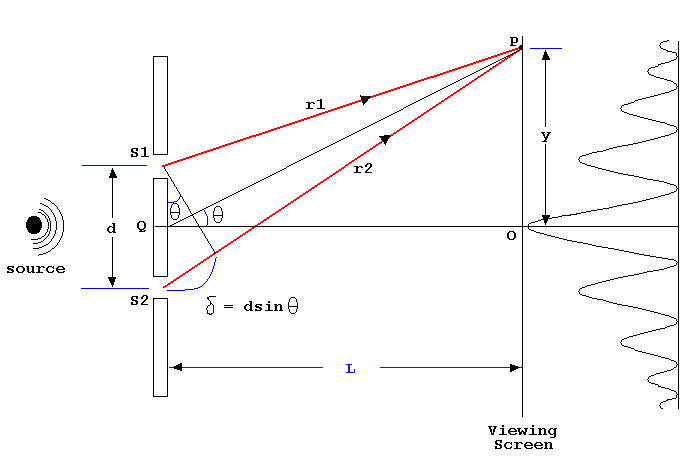
path difference.
A bright fringe can be found at points on the screen for which the path difference is equal to an integral multiple of the wavelength:
Since destructive interference occurs when waves arrive at the screen 180° out of hpase, dark fringes can be found when their path lengths differ by an odd integer multiple of a half wavelength:
|
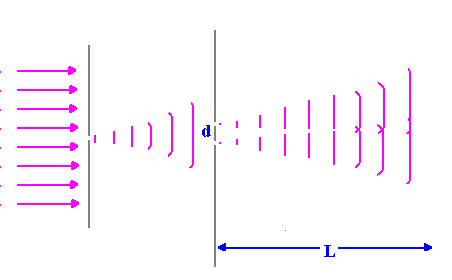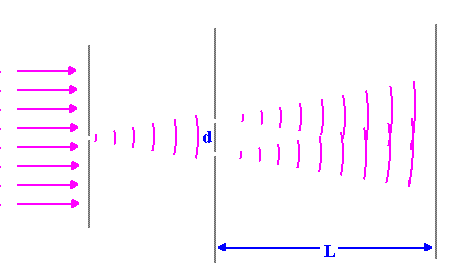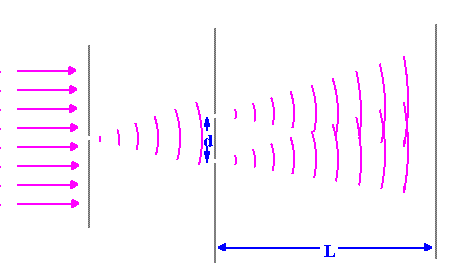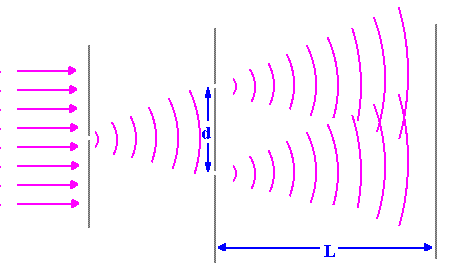
The position of the fringes are dependent of variables L, d and λ.
|
|
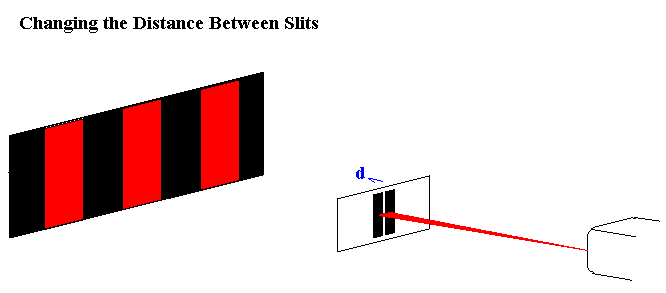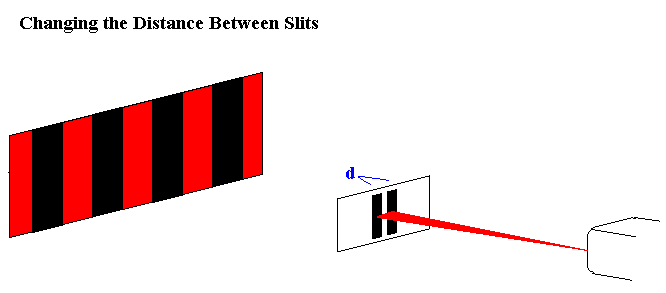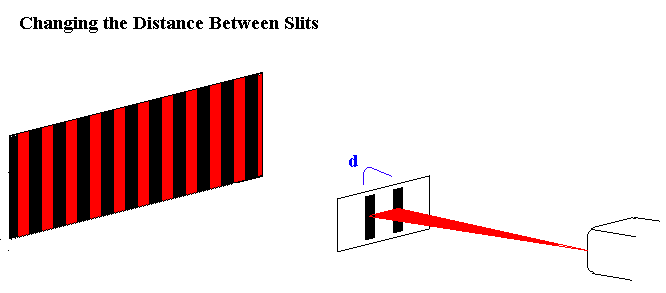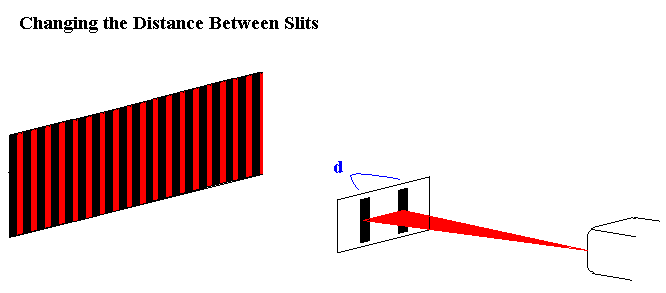
Increasing the length of d decreases the spacing between different fringes. This is consistent with the fact that spacings between different fringes inversely depend on d. This second diagram shows what happens to waves as they pass through the slits as d varies. More interference occurs when d is wider. |
  |
|
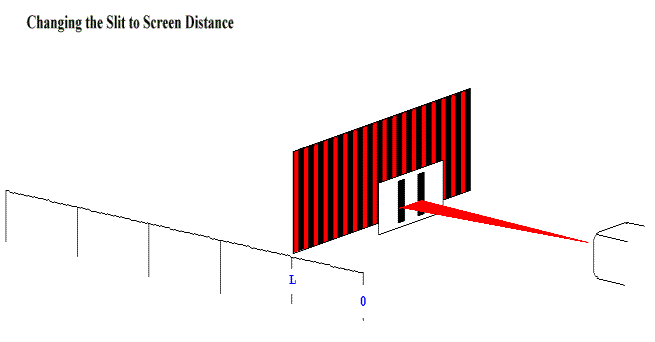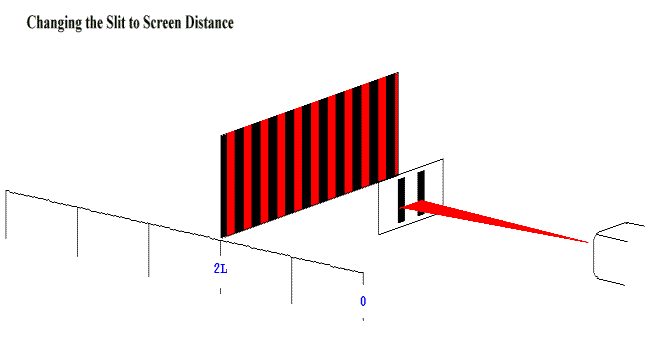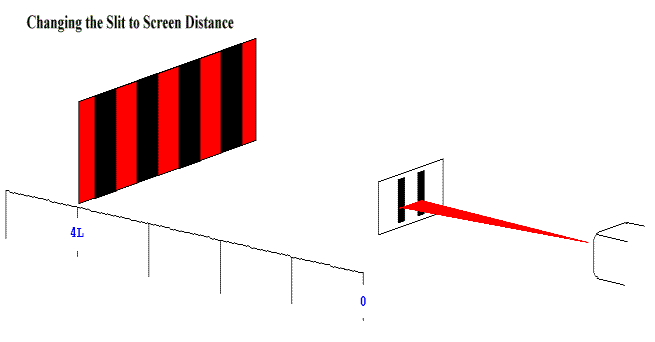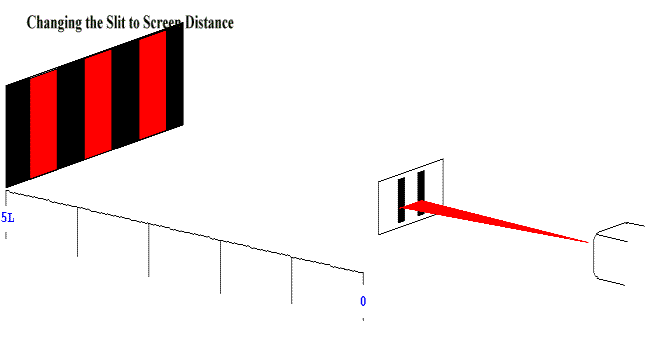
The spacings between different fringes decreases as the distance between the slits increases because it is dependent on L. |
 |
|
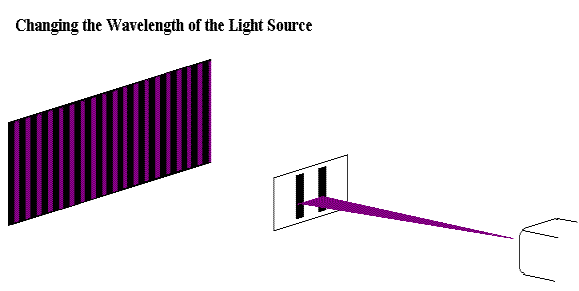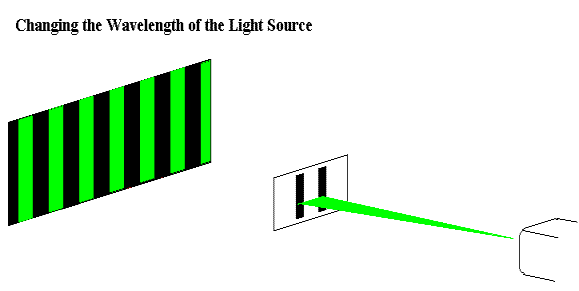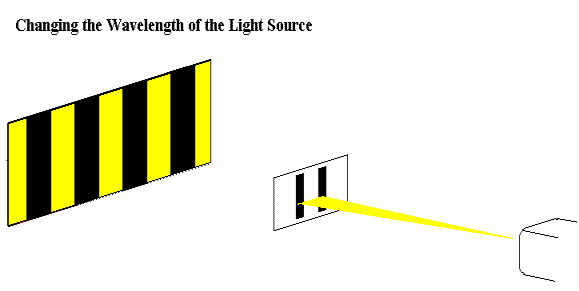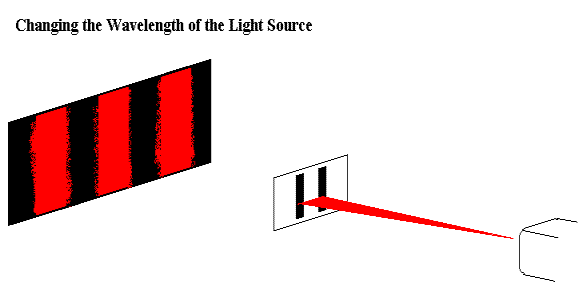
Increasing the wavelength of the light increases the spacing between different fringes since the spacing between different fringes is wavelength dependent. Red light has the largest wavelength of the color spectrum with a range of 625 - 740 nm, while violet has the smallest wavelength with a range of 380 - 435 nm. |
 |