Chromatic Aberration

   Chromatic Aberration occurs because of dispersion. Dispersion is the change in refractive index due to changing wavelength. The images formed from these different colours of light are not coincident. There are two effects of chromatic abberation
       1) Longitudinal displacement of the image along the optic axis ( Longitudinal Chromatic Abberation)
       2) Variation in image size with color (Lateral Chromatic Abberation)

This figure shows that, according to Snell's Law, the angle of refraction differ for different indexes.

Created by Postscript, edited with Paint, similar to class project but for one ray and for different index

A white object will not give rise to a white image but it will be distorted and have rainbow edges.

Created by Postscript,exaggerated index to illustrate the different focal due to wavelength

Connecting Wavelength to Indexes

Created by Paint, from class notes

Applying Huyen's Principle to Snell's Law :

The wavelengths are in Armstrong unit. These are the lines that appeared in the solar spectrum that J. von Fraunhofer studied known as "Fraunhofer wavelength". Created by Paint

The refraction index increased with an decreasing wavelengths. Created by Paint

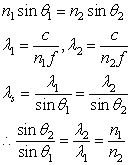
Using Linear Aproximation to illustrate Chromatic Aberration

We are going to find the matrices of a simple lens system and then determine the focal length with a given radii, distance between the lenses, and other information to shop that focal point differs for different wavelength

The Lens System Matrices

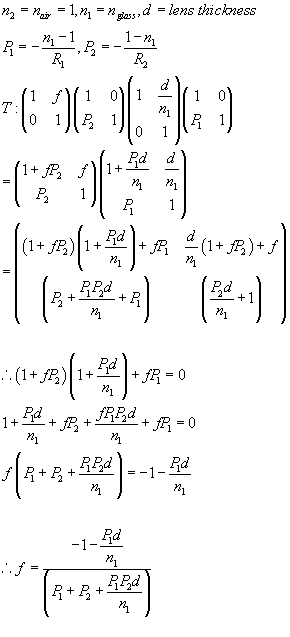
Examples

Example 1

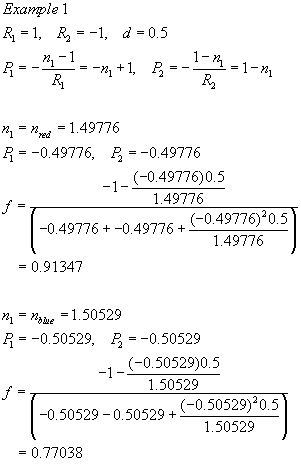
Example 2

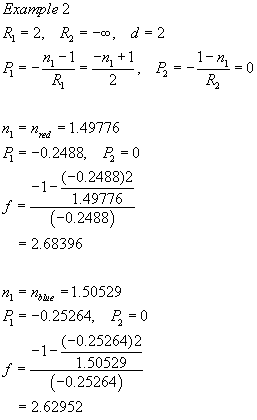
We have shown that the focal point is different for different colour due to the wavelength.

Correcting Chromatic Abberation:

Chromatic aberration can be eliminated by making multiple refracting elements with opposite power (Pedrotti). The most common solution is making a achromatic doublet, consisting a convex and a concave lens, of different glasses. For example, using a crown glass equiconvex lens to a negative flint glass lens.

Picture reproduced with Paint from Pedrotti

Design for thin len:

The matrix for thin len convex len is:

Let's apply the matrix to the matrix of a focus image, we get

Let's simplify the equation

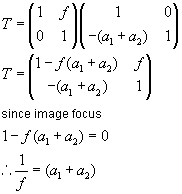
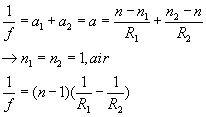
We are going to apply these equation to the sample achromatic doulet and figure out the lens design. The Fraunhofer wavelength we are going to use is D - yellow colour. Therefore, the index of refraction n is for the wavelength D.

The power of the two lens are

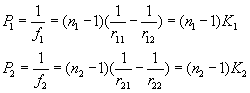
Let K1 and K2 be constants, represent abberation for the curvatures.

We know that the power of a doublet with a distance of L is

Since we our doublet are cemented, L=0, the powers are

According to Pedrotti(P. 101), chromatic aberration does not exist for yellow(D) wavelength if the power is independent of the wavelength or the derivative

We take the derivative of the power and we get

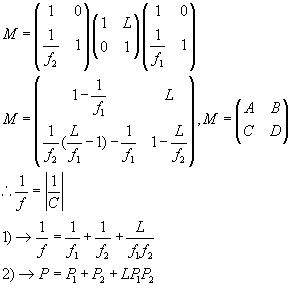
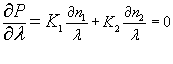
According to Blaker(p. 71), the dispersive power is v and dispersive constant V

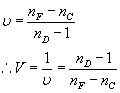
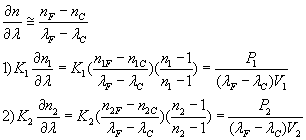
To determine the variation for n with lamda, in the area around the colour yellow, we have to take an approximation using the colour red and blue.

We want

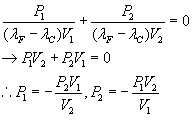
We have to determine each individual len power in term of the desire power P

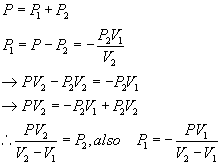
Finally, from the equation above, we can now determine the curvature K and the four radii.

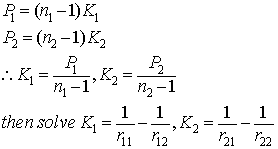
Achromatizing thin lens will result in a nearly equal focal lengths(focal length for red nearly equal to focal length for blue), eliminate longitudinal and later aberration at the same time, i.e will coincide. But the problem with thick len is that equal focal lenghts may not coincide as thin len. If we change the focal lengths for red and blue, resulting in a different later magnification and therefore lateral chromatic aberration remains. According to Pedrotti, the condition to remove lateral chromatic aberration is "the coincidence of the principal planes for the corrected wavelengths" (Pedrotti, p.104).