Name: Chan, Lai Shan (Sandy)

Student number: 94247970

Light Travels Through Slits

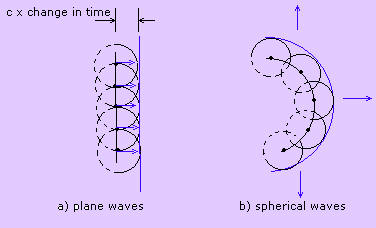
Christian Huygens, a Dutch scientist, was the first person to suggest that light can be a wave. Huygens' principle states that every point on a wave front acts as a source of tiny spherical wavelet that travels forward with the same speed, c , as the wave . At a later instant (an unit change in time), the new wave front is tangent to all the forward-propagating wavelets. According to the Huygens' principle, the propagation of plane and spherical waves travels like the picture shows below where a) is the plane waves and b) is the spherical waves.

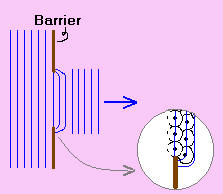
A light or a wave bends when it passes through an obstacle. This is called diffraction. When the waves are going through a slit/a barrier, Huygens' wavelets produced near the slit/the barrier edge cause the wave fronts to bend. Diffraction effect exists whenever a wave travels through a slit/a barrier. However, this effect is only important when the wavelength and the width of the slit have more or less the same length. We can illustrate that by the following two extreme cases.

Case II, when the width of the hole of the barrier and the wavelength are almost equal to each other, the wave fronts emerging from the hole spread in a broad pattern. In this case, the diffraction effect dominates the propagation. This is shown by the picture below:

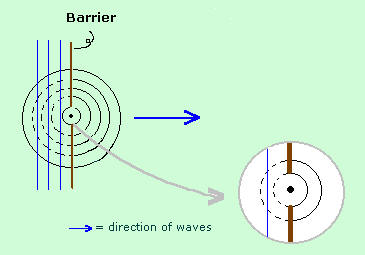
Therefore, we can ignore the diffraction effect and assume light travels through a medium in straight lines when we considered optical systems where dimensions are >> the wavelength of light.

Double-Slit Interference

The picture below is an example of how the waves travel when they pass through a pair of coherent sources with narrow slits.

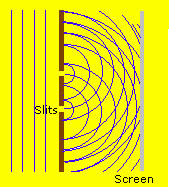
If we are going to map the intensity pattern along the slit some distance away, we'll find that it consists of bright and dark fringes. The bright light occurs when the paths from the 2 slits are either the same length or differ by an integer number of wavelengths which will form constructive interference (the waves are in phase under this condition). In contrast, the dark fringes occurs when their path length differ by an odd integer multiple of a half wavelength which will form destructive interference since it's 180 degree out of phase.

The picture below shows how we can find the locations of the interference fringes. A bright fringe occurs when the path-length difference (r2-r1) is an integer multiple of the wavelength.

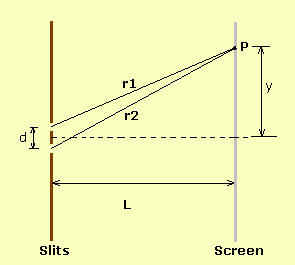
If we assume length L >> the slit distance d. Then, the path-length of r1 and r2 will travel nearly parallel to the point P on the screen. From the picture below (a zoom-in picture of the slits part of the above picture), we find that the length difference between r1 and r2 is equal to (d sin a).

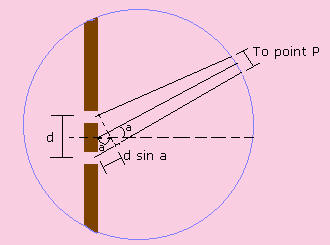
From what we illustrate above, we can find the location of bright fringes and dark fringes by the following two equations:

d sin a = m x wavelength (for bright fringes) where m=1,2,3....

d sin a = (m + 1/2) x wavelength (for dark fringes) where m=1,2,3....

References

G.R. Baldock and T. Bridgeman. Mathmetical Theory of Wave Motion. England: Ellis Horwood Limited, 1981.

Goran Einarsson. Principles of Lightwave Communications. England: John Wiley & Sons Ltd, 1996.

Mark P. Silverman. More Than One Mystery. New York: Springer-Verlag New York, Inc., 1995.