1 Me Me Me and Math

• Most of my course work for my Master's has centred around topology. I've completed a comprehensive in Analysis and a comprehensive in Algebra.
• I enjoyed reading through sections of Word Processing in Groups by David B. A. Epstein, J. W. Cannon, D. F. Holt, S. V. F. Levy, M. S. Paterson, W. P. Thurston.

My Master's essay was an introduction to kleinian groups. My supervisor for that was Bill Casselman. I looked into automatic groups and finite state machines. The main reading was the paper "Limit sets of free two-generator kleinian groups" (see a part of David Wright's page). There are two heads to these limit sets: algebra, and geometry. I wrote some programs to generate the limit sets. These programs exploit the algebra of the kleinian groups to produce the pictures. 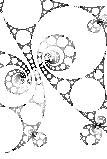The geometry introduced by Schotty groups explains the patterns you get--for instance whether it's connected or like cantor dust. In a way, the definition of Schottky groups describe a Iterated Function System that produces fractals. One of the big problems of with using the definition is that it is not clear how to retrieve a set of simple closed curves that satisfy the requirements if you start with the transformations. Since we are dealing with Möbius transformation it seem reasonable to just consider circles to be the curves in question unfortunately there are Schottky groups that can not be represented by circles--even for two-generator kleinian groups there are examples that need curves other than circles. One plausibly way to retrieve the curves would be to compute the limits and draw in two curves and throw them at the generators of the groups and see if they satisfy the properties of the Schottky group. This would seem to work and give you well behaved curves.