APMA990: Prelimary Project Results
Colin Macdonald, 01/03/2002
First of all, here is some simple code that helped me understand what
it was I expected from the Haar wavelet:
The output should be something like:
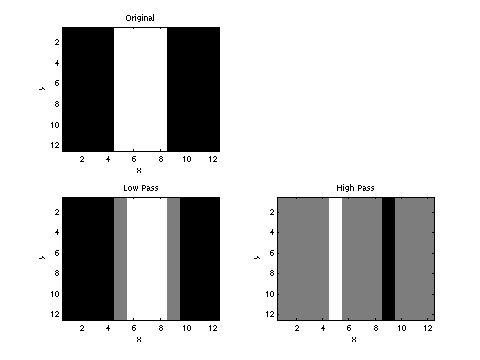
(by the way, all images on this page are .pngs: you
won't find any .gifs on this page because some lame company known as
UNISYS has a patent on them - see burnallgifs.org)
One thing worth noting is that the results of the high-pass filter
include both positive and negative values (measuring how much the
brightness is changing a local region of the image as we move from
left to right). For the purpose of exposition, we add the average
color (gray 32 in this case) to output from the high-pass filter.
After cleaning that code up a bit and modularizing a few things, I was
able to use this code run the Haar wavelet
recursively to generate images like this:

Notice that there are lots of gray areas with very little change. This made me think about lossless compression, namely:
- We can in theory losslessly undo the wavelet filters to obtain the original picture (in practice, I seem to encounter problems due to rounding but maybe I have a bug in my code...)
- Perhaps a simple lossless compression technique can a acheive a better compression ratio for the image after its passed through the wavelet filters as compared to the original image.
To test this, I used the "Lena" image and ran the wavelet filter recursively to various depths and saved the files as a raw uncompressed image format (.bmp). These raw files where then compressed with a general purpose compression tool (gzip) and the resulting file sizes shown in the following figure:
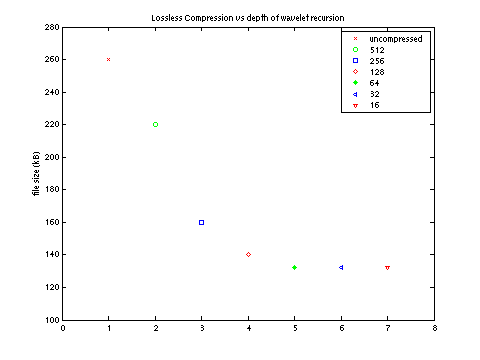
(The level of recursion is measured by the size of the smooth Lena image in the upper left corner (i.e., 128 in the Lena figure above).)
It seems that we can almost double the compression ratio for this particular image. Not bad at all!
More to follow...


