Level curves

Scroll down to the bottom to view the interactive graph.

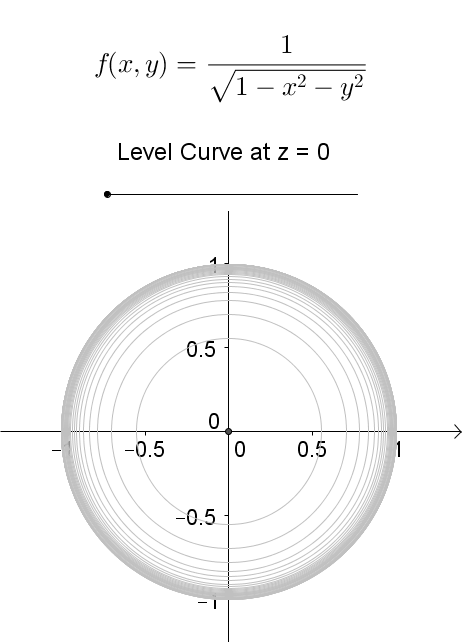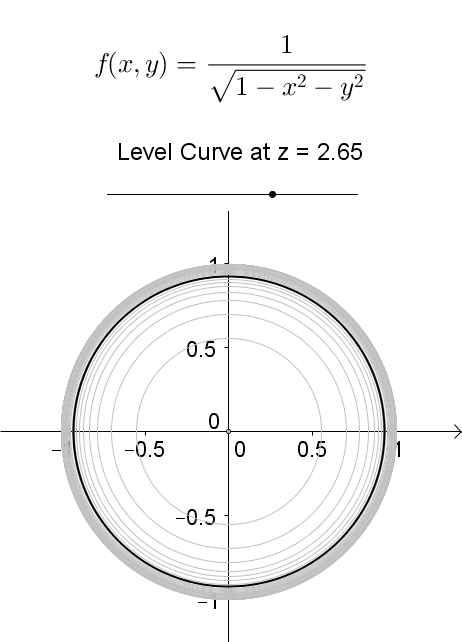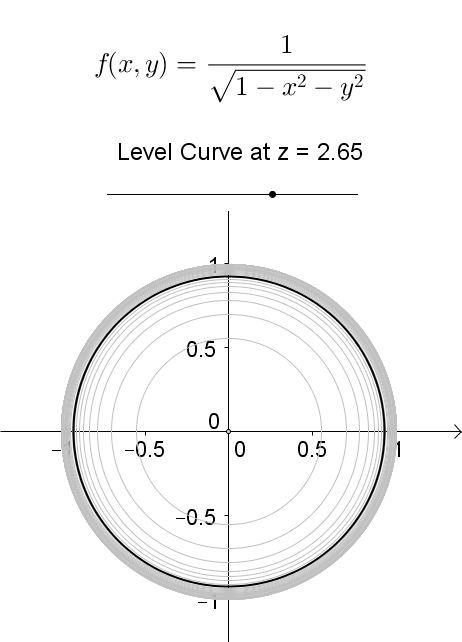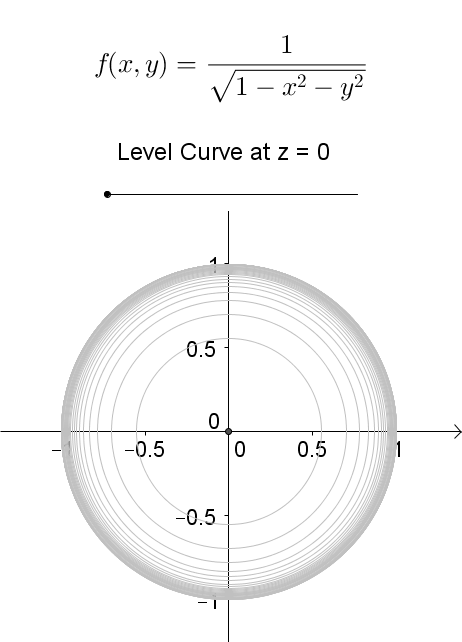
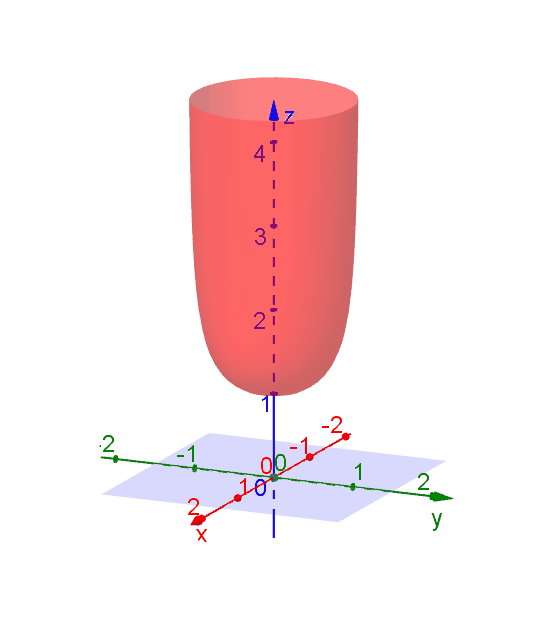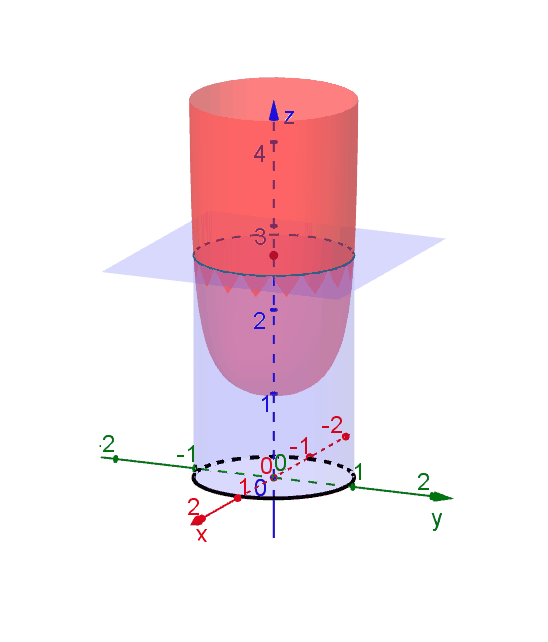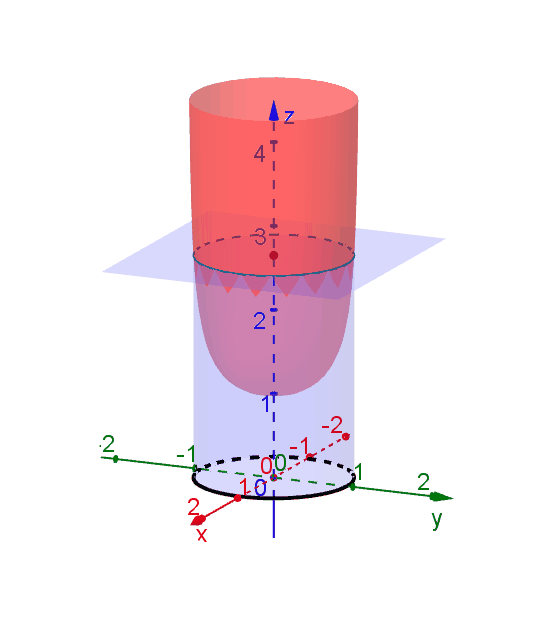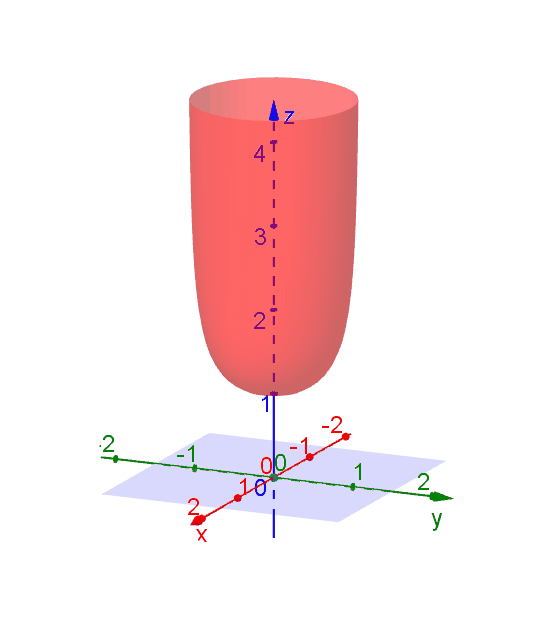
A level curve of \(f(x,y)\) is a curve on the domain that satisfies \(f(x,y) = k\). It can be viewed as the intersection of the surface \(z = f(x,y)\) and the horizontal plane \(z = k\) projected onto the domain. The following diagrams shows how the level curves \[f(x,y) = \dfrac{1}{\sqrt{1-x^2-y^2}} = k\] changes as \(k\) changes. Note that the level curves are circles given by \[x^2 + y^2 = 1-\dfrac{1}{k^2}\] for \(k \ge 1\), for which the radii never exceed 1. For \(k < 1\), the plane \(z = k\) does not intersect with the surface and hence there are no level curves.

To view the interactive graph:

1. Make sure you have the latest version of Java 7 installed in your computer. Tablets and smartphones are not supported.
2. Download this file, levelcurve.ggb.
3. Click here to open GeoGebra.
4. After you open GeoGebra, click "File" in the toolbar, then click "Open".
5. Choose the .ggb file you just downloaded and click the "Open" button.
6. Now you should be able to view the graph inside GeoGebra.

To rotate the graph, right click and drag.

Joseph Lo