Tangent plane

Scroll down to the bottom to view the interactive graph.

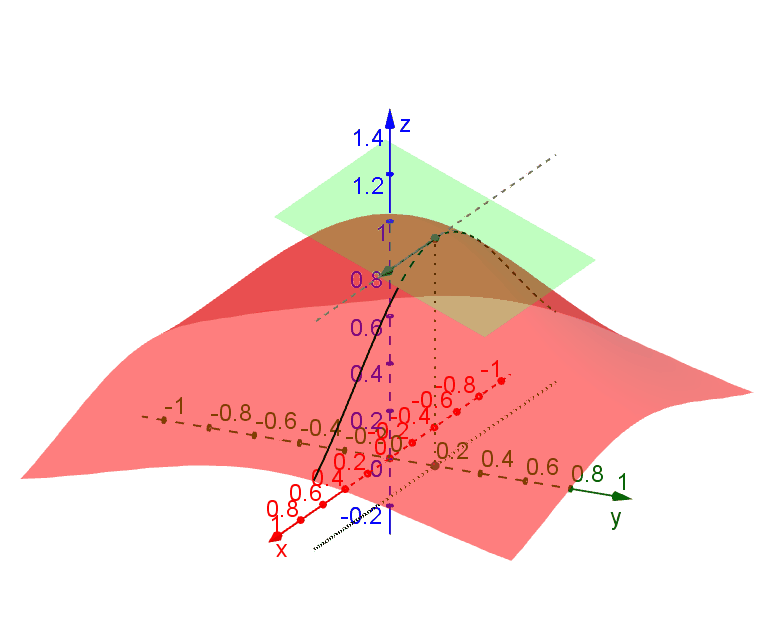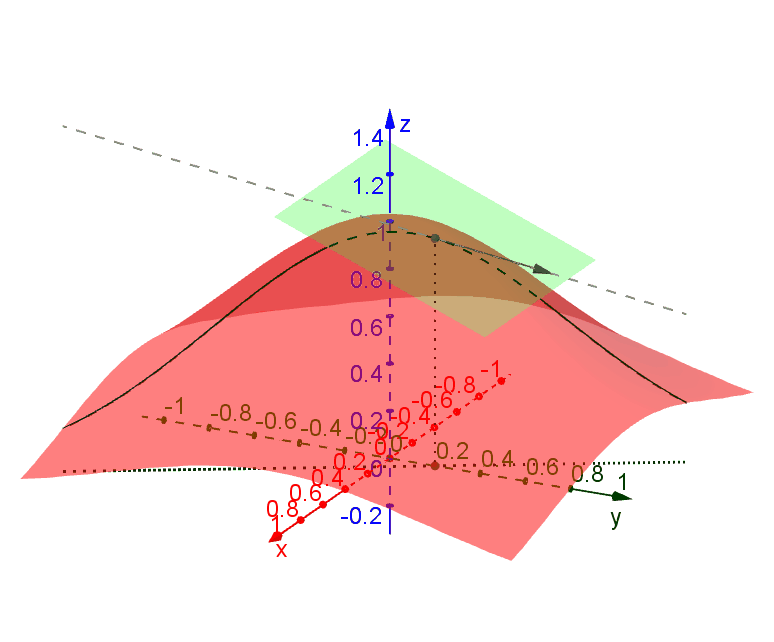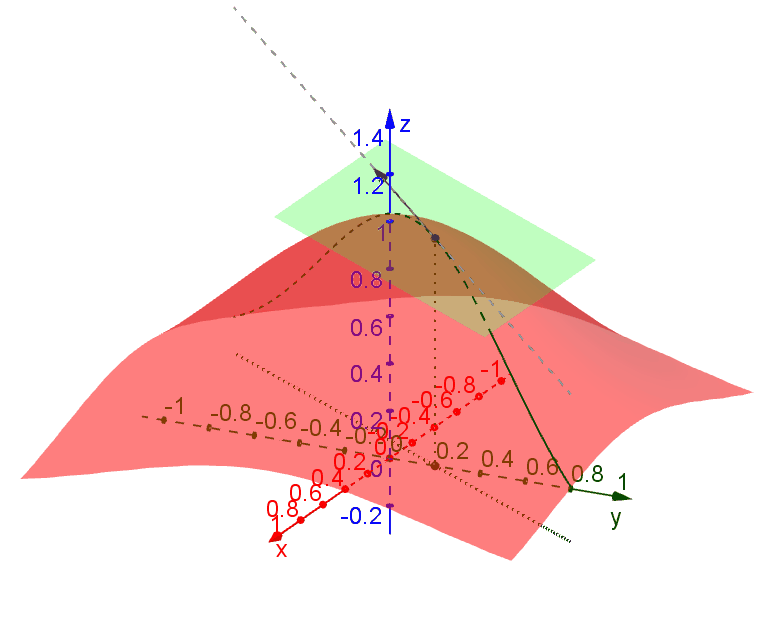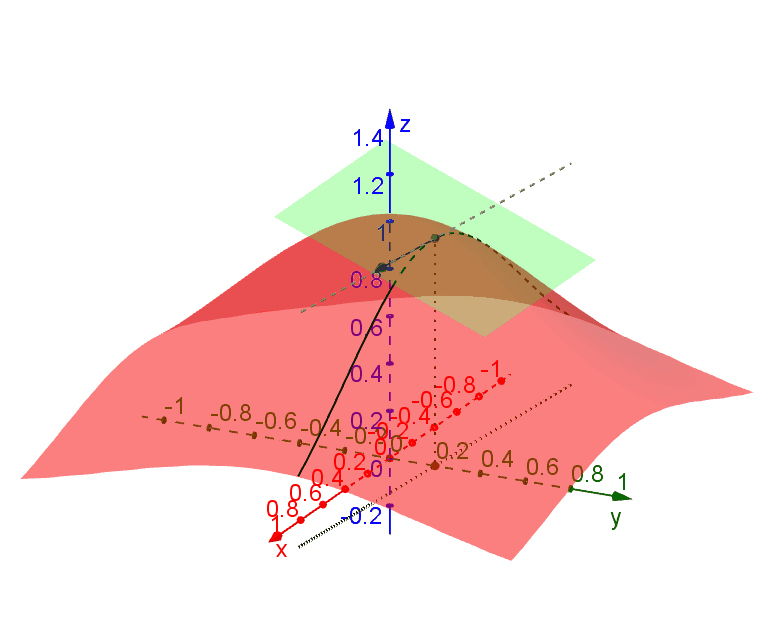
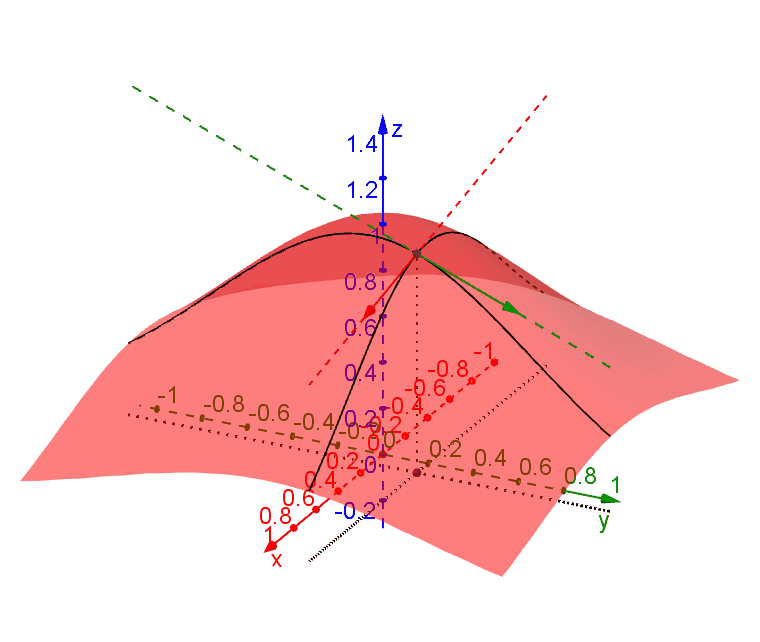
A tangent plane to a function \(f(x,y)\) at a point \(P (x_0,y_0)\) is the plane which contains all tangent lines along all traces through \(P\). The following diagram illustrates this idea.

We say that \(f(x,y)\) is differentiable at \(P(x_0,y_0)\) if such a plane exists at \(P\). In this case we can find the plane by using only the trajectories parallel to the \(xz\)-plane and the \(yz\)-plane.

To view the interactive graph:

1. Make sure you have the latest version of Java 7 installed in your computer. Tablets and smartphones are not supported.
2. Download this file, tangentplane.ggb.
3. Click here to open GeoGebra.
4. After you open GeoGebra, click "File" in the toolbar, then click "Open".
5. Choose the .ggb file you just downloaded and click the "Open" button.
6. Now you should be able to view the graph inside GeoGebra.

To rotate the graph, right click and drag.

Joseph Lo