Anatomy of Triangles

Part of the Geometry Primer for Mathematics 337 at the University of British Columbia.
A triangle has, of course, three vertices, three sides, and three angles. But it has further threesomes which do not meet the eye quite as readily. If you draw three lines at random, chances are that they will yield the sides of some triangle: it would be unusual if they met in a single point. But that is what happens with the following triples of lines, which are associated with any triangle.

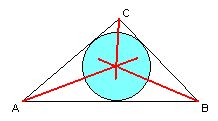
If you move from the vertex A into the triangle ABC, always making sure that your distance to the side AB is the same as that to AC, you are cruising along the angle bisector of A. Similarly, every point on the angle bisector of B is equidistant from the sides AB and BC. The point J of intersection of these two angle bisectors is therefore equidistant from all three sides. Hence the angle bisector of C must also go through J -- see? -- and J is the centre of the inscribed circle of the triangle.

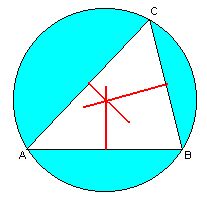If you move from the side AB into the triangle ABC, always making sure that your distance to the vertex A is the same as that to B, you are cruising along the perpendicular bisector of AB. Similarly, every point on the perpendicular bisector of BC is equidistant from the vertices B and C. The point K of intersection of these two perpendicular bisectors is therefore equidistant from all three vertices. Hence the perpendicular bisector of CA must also go through K -- see? -- and K is the centre of the circumscribed circle of the triangle.
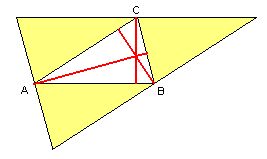
A perpendicular from a vertex to the opposite side is called an altitude of the triangle; it runs inside the triangle if and only if the angles at the other two vertices are both acute (see?).

The altitudes of a given triangle ABC are just the perpendicular bisectors of its fourfold enlargement, as shown. Hence the three of them meet in a single point H -- namely the "circumcentre" of the enlargement.

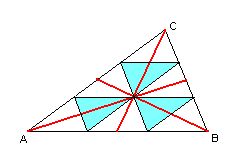By trisecting all sides, any triangle can be subdivided into nine smaller ones, as shown. If you move from the vertex A toward the intersection M of the three blue triangles, you are cruising along the diagonal of a little white and blue parallelogram, and if you continue beyond M, you echo the first half of your trip (through the white triangle at A). You will therefore arrive at the midpoint of the side BC.
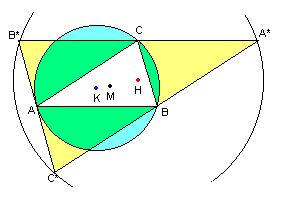The line connecting a vertex to the midpoint of the opposite side is called the median of that side, and the description just given shows that the three medians go through the same point M -- which lies two thirds of the way along each median. M is known as the centroid of the triangle.

Bisectors, medians, and altitudes occur in many parts of the theory of triangles. So do the three points (namely K, M, and H) which are the subject of our next and last example -- but the most surprising fact about them seems to be more of a curiosity:
K, M, and H lie on a single line, with MH twice as long as KM. The line containing them is named after the great eighteenth century mathematician Leonhard Euler.

The point M is the centroid of both the triangle ABC and its enlargement A*B*C*. As we have seen above, the intersection H of the altitudes is also the circumcentre of the triangle A*B*C*, so it would make sense to write H=K*.

Consider the following transformation of the plane: with M as the centre, turn the plane through 180 degrees and simultaneously double the distance of every point from M. How would this affect the points A,B, and C? How does it explain the mystery of Euler's line? ***********************************************************************