He came very close to the 40,000 km we now accept as the true circumference. How did he do it? How is it possible that Columbus (1750 years later) did not know it?
 |
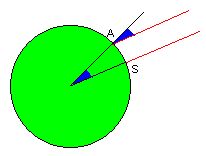
This is how Eratosthenes measured the girth of the earth
in about 250 BC. He heard about a well in Syene
(south of Alexandria), whose bottom was reached by the sun
only once a year. He found out the distance to Syene and,
come that time the following year, measured the shadow of
a pole near his house in Alexandria ...
He came very close to the 40,000 km we now accept as the true circumference. How did he do it? How is it possible that Columbus (1750 years later) did not know it? |
| The most important ingredients in his considerations were: (a) any two sun-rays reaching the earth at the same moment are practically parallel; (b) if a straight line cuts a pair of parallels, it creates a lot of equal angles (e.g. the blue ones). This one of the "axioms" of plane geometry. How could (a) have been tested? | 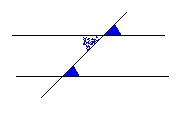 |
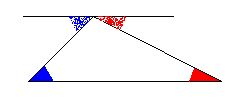 |
One of the almost immediate consequences of that axiom is the fact that the angles in a triangle add up to a "straight angle" (i.e. 180 degrees). Do you see why? |
|
Another version of basically the same fact is that
an "exterior angle" at one vertex of a triangle
equals the sum of the interior angles at the two
other vertices. Can you make the connection?
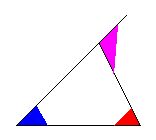
This observation is often applied to the case of isosceles triangles: the exterior angle at the summit is double the base angle. |
 |
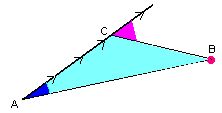 |
The following trick, called "doubling the angle at the bow" is still used in sailing. You stand aft (at A) looking toward the bow and keep track of the angle between that direction and the line of sight to a point B on the shore. When the angle has doubled (at C), you are as far from B as from A (which you know from your speed and the time elapsed). |
|
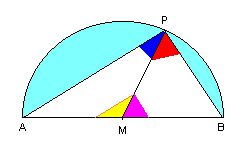
Another related fact often used in geometry is commonly
ascribed to Thales of Miletus: seen from any point P on a
semi-circle, the end points of the corresponding diameter
appear to be 90 degrees apart.
Reason: the blue (red) angle at P equals half of the purple (yellow) angle at M. Since the purple and yellow angles add up to 180 degrees, the blue and red add up to 90. |
 |