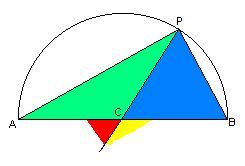
the green (blue) angle at P equals half of the red (yellow) angle at centre C of the circle. Hence the green and blue angles at P add up to one half of the sum of the red and yellow angles (which is 180 degrees).
|
Let us reconsider the argument which proves that a right
angle is formed whenever we connect any point P on a
semi-circle with the two end points A and B of its base:
the green (blue) angle at P equals half of the red (yellow) angle at centre C of the circle. Hence the green and blue angles at P add up to one half of the sum of the red and yellow angles (which is 180 degrees). |
 |
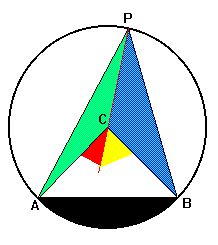 |
Except for its last parenthesis, this argument carries
over verbatim to segments AB
which are not necessarily diameters of the circle -- as long as
the point P does not wander off too far to the left or the right;
more precisely, as long as C still lies inside the triangle ABP.
Upshot: the angle APB at the circumference is exactly half of the angle ACB at the centre. In other words, keeping A and B fixed, you can move P around without changing the angle at the top. This unexpected result would be an even nicer theorem without that awkward restriction on the movement of P. |
|
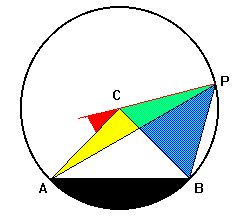
In fact, the desired theorem does hold! However, if C lies
outside the triangle ABP, the picture is quite different -- but if
you switch your thinking from adding to subtracting, you will see
a similar logical pattern.
It must be shown that the yellow angle at C equals twice the blue one at P. The latter is the difference between the blue one at B and the yellow one at A -- base angles of the isosceles triangles PCB and PCA. The exterior angles at C of the same triangles are twice as big. They are the red and yellow angle for PCB and the thin red one for PCA -- and their difference is just the yellow angle at C. |
 |
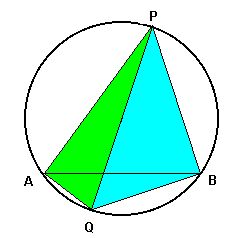 |
What about a point Q on the other side of AB, where the circular
segment is less than a semi-circle?
This is easily answered in terms of the point P diametrically opposite Q: the angle AQB is just the supplement of our old friend BPA. Indeed the green and the blue triangles shown here have right angles at A and B, respectively, hence their angles at P and Q add up to 90 degrees. The total angles (green and blue together) at P and Q therefore add to 180 degrees. Summary: all angles on one side of a circular segment are equal, and are supplementary to the angles on the other side of that segment. |