The resulting six wedges can then be arranged into a rectangular strip marked with a zig-zag pattern -- like so.
Heron of Alexandria lived in the first century BC and contributed massively to mechanics, optics, and geometry. Today he is mainly remembered for a remarkable way of computing the area of a triangle (Heron's Formula) -- namely as the square root of a four-dimensional volume! A bold stroke -- which we shall hide by jumping from shapes to numbers before we get to the famous formula.
 |
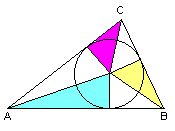
For the moment -- staying with shapes -- let us consider a triangle
ABC decomposed as shown on the left by
cutting along the angle bisectors and the perpendiculars dropped
onto the sides from the centre of the inscribed circle.
The resulting six wedges can then be arranged into a rectangular strip marked with a zig-zag pattern -- like so. |
| First question: given a strip subdivided as on the right, with obtuse angles LAM and AMB, how can one tell (without taking it apart) that its pieces can be assembled into triangle as shown above? | 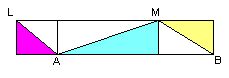 |
By the way, if angle AMB were not obtuse, the angles around M in the next diagram below would add to at most 180 degrees (see?), and there would no "crater" at M to fit the purple wedge and its twin. Likewise for LAM.
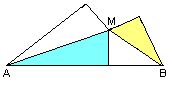 |
It is easy to begin assembling the desired triangle; the only question is whether the angles on the purple wedge are correct. In other words: do the angles ALM, MAB, and MBA add up to 90 degrees? One could just measure the angles and check -- but Heron does better... |
|
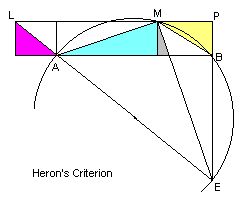
Here is Heron's Criterion: the wedges of the strip can be assembled into
a triangle as shown, if and only if the extended line LA goes through the
circumcentre of the triangle ABM.
The argument takes place almost entirely inside the circumcircle of AMB. If AE is its diameter through A, a right angle AME (green and gray) is formed at M. The other angles at M -- namely EMB, AML (=MAB), and PMB (=MBA) -- add up to 90 degrees. Hence all is well if and only if angles EMB (=EAB) and ALM are equal. |
 |
The same result can be formulated in various ways. Without reference to
a circle, it may be stated like this: let E be the intersection
of the lines LA and PB; then the wedges of the strip can be assembled into a
triangle, if and only if AME is a right angle.
For this version, the argument would start with the circumcircle of ABE.
The rightness of AME means that M also lies on this circle, and then
everything follows as before.
| Yet another version -- which refers to nothing outside the strip -- involves the point R opposite M on the strip and the point O where the lines AB and ME intersect. Without mentioning E, it goes as follows. | 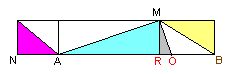 |
 |
Let the point O be chosen so that the
linear triples ROB and NAB are similar; then the wedges of the strip can
be assembled into a triangle, if and only if AMO is a right angle.
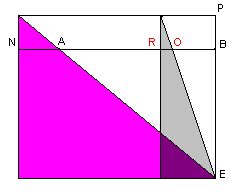
The connection between this statement and the previous one is made by the diagram on the left. It is derived from the one with the circumcircle by completing the triangle LEP to a rectangle and omitting all inessential features. It clearly shows that the linear triples NAB and ROB are both similar to PBE, hence to each other. |
Exercises. Given a strip with only one of the points A or M marked on it, find the other point, and then verify that the resulting zig-zag pattern can actually be cut out and turned into a triangle.