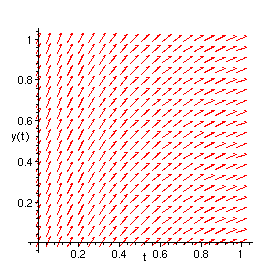
>
DEplot({diff(x(t),t)=1,diff(y(t),t)=x(t)},[x(t),y(t)],t=0..2,{[x(0)=0,y(0)=1]},linecolour=blue,thickness=1,
arrows=none);
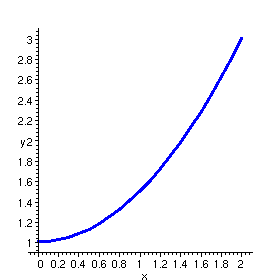
A work-around is to use subs on the result of DEplot as follows:
> subs(THICKNESS(3)=THICKNESS(1),");
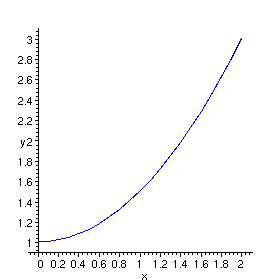
This bug has been corrected in Release 5.
> DEplot({diff(x(t),t)=1, diff(y(t),t)=x(t)}, [x(t),y(t)], t=0..1, [[x(0)=1,y(0)=1]], scene=[t,x]);
Error, (in DEtools/DEplot/CheckDE) invalid subscript selector
A direction field only makes sense here with scene=[x,y] . Nevertheless, you must specify arrows=none to indicate that you don't want it.
> DEplot({diff(x(t),t)=1, diff(y(t),t)=x(t)}, [x(t),y(t)], t=0..1, [[x(0)=1,y(0)=1]], scene=[t,x],arrows=none);
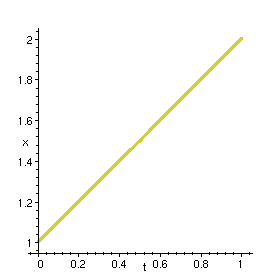
This bug has been corrected in Release 5.
>
DEplot({diff(r(t),t)=-sin(theta(t)/2), diff(theta(t),t)=1/2},
[r(t),theta(t)], t=0..3,
[[r(0)=1,theta(0)=0]], arrows=none,coords=polar);
Error, (in plot/options2d) unknown or bad argument, coords = polar
>
DEplot3d({diff(r(t),t)=-sin(theta(t))/2, diff(theta(t),t)=1/2},
[r(t),theta(t)], t=-0..3,
[[r(0)=1,theta(0)=0]], scene=[r,theta,t],
coords=cylindrical);
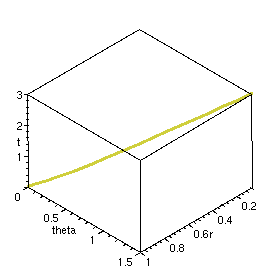
A work-around is to produce a list of points, and plot it using plot (in two dimensions) or spacecurve (in three dimensions).
>
L1:= op(indets(DEplot({diff(r(t),t)=-sin(theta(t)/2), diff(theta(t),t)=1/2},
[r(t),theta(t)], t=0 .. 3,
[[r(0)=1,theta(0)=0]],arrows=none),list(list(numeric)))):
> plot(L1,coords=polar,scaling=constrained);
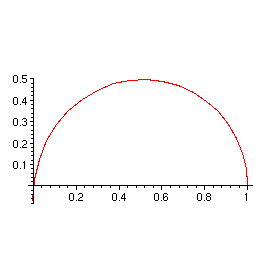
>
L2:= op(indets(DEplot3d({diff(r(t),t)=-sin(theta(t))/2, diff(theta(t),t)=1/2},
[r(t),theta(t)], t=-Pi..Pi,
[[r(0)=1,theta(0)=0]], scene=[r,theta,t]),list(list(numeric)))):
> plots[spacecurve](L2,coords=cylindrical);
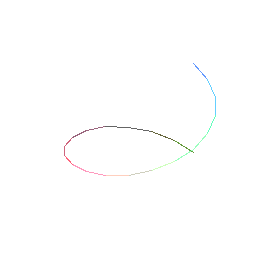
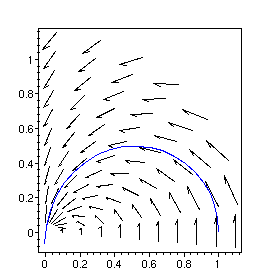
This can be done for the direction field too (if you don't mind a bit of distortion in the arrows). In order to have the direction field and trajectories in different colours, they should be plotted separately and combined using display .
>
L3:= {op(indets(DEplot({diff(r(t),t)=-sin(theta(t)/2), diff(theta(t),t)=1/2},
[r(t),theta(t)], t=0 .. 3, r=0.1 .. 1.1,theta=0 .. 1.55, dirgrid=[10,8]),list(list(numeric))))}:
>
p1:= plot(L1, coords=polar, colour=blue):
p2:= plot(L3, coords=polar, colour=black):
plots[display]({p1,p2},scaling=constrained,axes=box);
>
DEplot({diff(x(t),t) = y(t)*x(t), diff(y(t),t) = 0}, [x(t),y(t)], t=0..0.5, x=0..1, y=-1..1, arrows=SMALL);
Error, (in DEplot) Cannot produce plot, non-autonomous DE(s) require initial conditions.
> DEplot({diff(x(t),t) = y(t), diff(y(t),t) = 0}, [x(t),y(t)], t=0 .. 0.5, {[x(0)=.5,y(0)=.5]}, x=0..1, y=-1..1, arrows=SMALL);
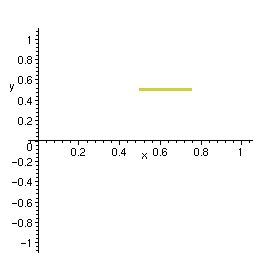
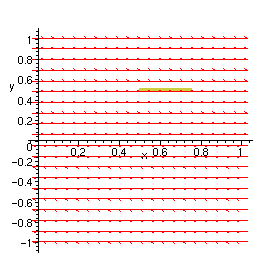
A work-around is to use a very small but nonzero value for the derivative.
> DEplot({diff(x(t),t) = y(t), diff(y(t),t) = 0.0001*y(t)}, [x(t),y(t)], t=0 .. 0.5, {[x(0)=.5,y(0)=.5]}, x=0..1, y=-1..1, arrows=SMALL);
>
DEplot(diff(y(t),t) + y(t) = 1, y(t), t=0..1, [[y(0)=2]]);
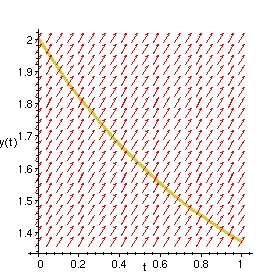
The work-around is to rewrite the differential equations to put everything except derivatives on the right side.
> DEplot(diff(y(t),t) = 1 - y(t), y(t), t=0..1, [[y(0)=2]]);
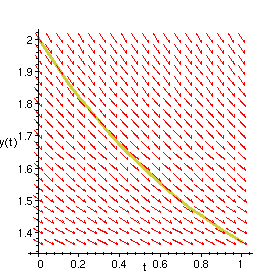
This bug has been corrected in Release 5.
> DEplot(diff(y(t),t) = exp(1-2*t), y(t), t = 0 .. 1,y=0..1);
Plotting error, non-numeric vertex definition
In this case, the problem doesn't occur if a floating-point value is placed inside the exp .
> DEplot(diff(y(t),t) = exp(1.0-2*t), y(t), t = 0 .. 1,y=0..1);
Another work-around is to map evalf into every CURVES structure in the DEplot result.
>
pl:= DEplot(diff(y(t),t) = exp(1-2*t), y(t), t = 0 .. 1,y=0..1):
pts:= indets(pl,specfunc(anything,CURVES)):
s:= map(t -> (t = map(evalf,t)), pts):
subs(s,pl);