Advice: Errors in symbolic integration
As most calculus students know, integration can be a difficult process. Even in Maple, the difficulties have not all been overcome, and symbolic integration should not be considered as completely reliable in all cases. In general it is prudent to check the correctness of integrals, either by comparing definite integrals to their floating-point approximations or by comparing the derivative of an indefinite integral to the integrand.
One common source of trouble is multivalued functions. In particular, a definite integral
int(f(x), x = a .. b)
may give a wrong answer because the antiderivative is a multivalued function
![]() with a branch cut crossing the path of integration. Maple may not recognize the branch cut, and return
with a branch cut crossing the path of integration. Maple may not recognize the branch cut, and return
![]() as the value of the definite integral. Note that this can happen even when the integrand
as the value of the definite integral. Note that this can happen even when the integrand
![]() is single-valued.
is single-valued.
In other cases, when
![]() is multivalued Maple may find an antiderivative for the wrong choice of branch of
is multivalued Maple may find an antiderivative for the wrong choice of branch of
![]() .
.
Examples:
The following example is in Maple 6 as of January 2000. It may be corrected in later releases.
We begin with the function
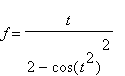 and its antiderivative
. Note that
and its antiderivative
. Note that
![]() is continuous on the whole real line.
is continuous on the whole real line.
> f:= t/(2-cos(t^2)^2);
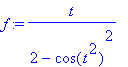
> F:= simplify(int(f,t));
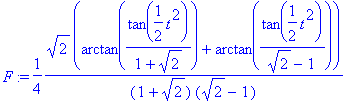
This is correct in the sense that the difference between
![]() and the derivative of
and the derivative of
![]() simplifies (with a little help) to 0.
simplifies (with a little help) to 0.
> simplify(diff(F,t)-f);
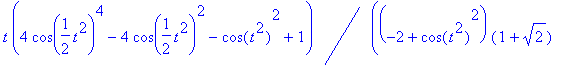
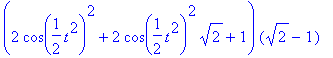
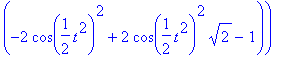
> combine(%,trig);
![]()
Here is a definite integral with this integrand.
> J1:=int(f, t= 0 .. 2);
![]()
> evalf(J1);
![]()
This result is equivalent to that obtained by evaluating the antiderivative at the endpoints of the interval.
> simplify(eval(F,t=2)-eval(F,t=0) - J1);
![]()
However, the answer is wrong (rather obviously, because the integrand is positive on this interval). Here is the correct value, obtained by numerical integration.
> evalf(Int(f, t=0 .. 2));
![]()
> err:= % - evalf(J1);
![]()
The cause of the error is a discontinuity of the antiderivative at
![]() . It has a jump of size equal to the error.
. It has a jump of size equal to the error.
> evalf(limit(F,t=sqrt(Pi),left)-limit(F,t=sqrt(Pi),right));
![]()
The next example features a problem with branches of a fractional power.
> f:=((2-3*x)^(-2)*x^(-8))^(1/5);
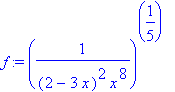
> F:= int(f,x);
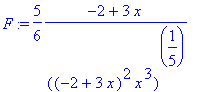
> simplify(diff(F,x));
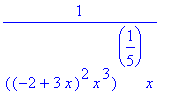
This is the same as
![]() for positive
for positive
![]() , but not for negative
, but not for negative
![]() (with the principal branch of the fifth root, which Maple uses).
(with the principal branch of the fifth root, which Maple uses).
> evalf(subs(x=-1,diff(F,x)));
![]()
> evalf(subs(x=-1,f));
![]()
See also: int , Integrals involving fractional powers , Numerical integration
Maple Advisor Database R. Israel, 1998