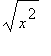Advice: Assume doesn't affect solve

The assume command is used with symbolic variables that are not assigned values, and tells Maple that it can apply rules that would be appropriate when the variable has certain properties (e.g. is an integer). This primarily affects the simplify command. Thus if x is assumed to be positive, 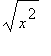can be simplified to .

However, these assumptions do not restrict the values for x that can be returned by solve and its related commands. There are other ways to restrict these values.

Examples:

> assume(x, positive);

> simplify(sqrt(x^2));

In this example, solve finds both real and complex solutions; the assumption on x has no effect.

> solve(x^4 + 2*x = 20, x);

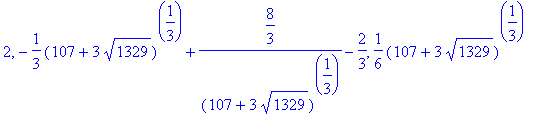
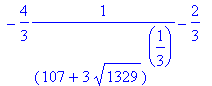
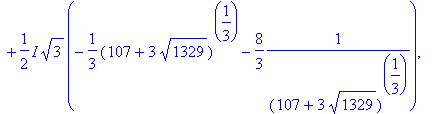
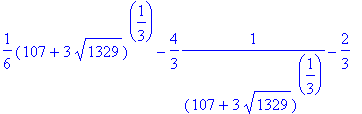
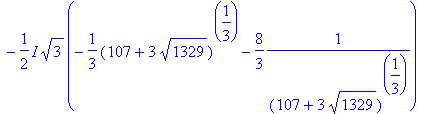
Finding positive solutions in "solve":

> solve({y^4 + 2*y = 20, y > 0}, y);

Finding real solutions:

> solve({y^4 + 2*y = 20, y > -infinity}, y);

Finding integer solutions:

> isolve(y^4 + 2*y = 20);

Real (numerical) solutions with fsolve :

> fsolve(y^4 + 2*y = 20, y);

Restricting to an interval:

> fsolve(y^4 + 2*y = 20, y = 0 .. infinity);

Another option for fsolve is avoid = {variable = value, ...} which causes fsolve to omit one or several known solutions. This is especially useful for non-polynomial equations where fsolve only returns one solution.

> fsolve(y^3 + 2 = 20/y, y);

> fsolve(y^3 + 2 = 20/y, y, avoid = {y=2});

However, the avoid option doesn't seem to work for systems of equations:

> fsolve({x+2*y=2,x^2-y^2=0},{x,y}, avoid={x=-2.000000000,y=2.000000000});

> fsolve({x+2*y=2,x^2-y^2=0},{x,y}, x=0..infinity);

Maple Advisor Database R. Israel, 1997