Advice: Defining functions

Here is a correct way of defining a function:

> f:= x -> x^2 + 1;

You can then evaluate such a function with a constant or variable argument:

> f(u);

> f(3);

Similarly, for a function of several variables (note the parentheses):

> g:= (x,y) -> x+y^2;

> g(u,v);

On the other hand, the following defines an expression rather than a function:

> h:= x^2 + 1;

This is no problem if that's what you wanted, but functions and expressions are used in different ways. In particular, you get a strange-looking result if you try to evaluate h as you would a function:

> h(u);

In order to evaluate h for some value of x , you must use subs or eval .

> subs(x=u, h);

> eval(h,x=u);

Since in ordinary mathematics we often speak of "the function 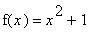", a common beginner's mistake is to define f(x) instead of defining f .

> F(x):= x^2 + 1;

Beware! Everything seems fine, as long as you use only F(x) . But when you try to use F with some other argument, it appears to be undefined:

> F(u);

This is not surprising, since in fact it is only F(x) , and not F of anything else, that you have defined. There is a legitimate use of such a construction (it places a value in the remember table of F ).

See also: function , remember , subs

Maple Advisor Database R. Israel, 1997