Bug fix: Residue returns 0
The function residue computes the residue of an analytic function at a pole of the function.
> residue(sin(z)/z^2,z=0);
![]()
In some cases residue returns an incorrect answer of 0.
>
f:= x/(1+x^7): p:= cos(Pi/7)+I*sin(Pi/7):
residue(f,x=p);
![]()
>
pr:= RootOf(1+Z^7);
residue(f,x=pr);
![]()
![]()
This is usually due to the series command not recognizing that the denominator is 0 at the given point.
> series(f,x=p,1);
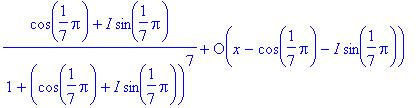
> series(f,x=pr,1);
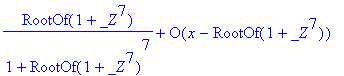
Sometimes this problem can be helped by using a different representation of the point
![]() . In this case using complex exponentials instead of sines and cosines would work.
. In this case using complex exponentials instead of sines and cosines would work.
> residue(f,x=convert(p,exp));
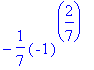
Another possibility which sometimes works is to change the environment variable Testzero , whose value is the procedure used in series to determine when the leading coefficient is 0. By default this uses Normalizer , another environment variable whose default value is normal . Since residue and series have the remember option, we must use forget to remove results obtained using Normalizer from their remember tables.
>
Testzero:= proc(O) evalb(simplify(O)=0) end:
forget(series);
forget(residue);
residue(f,x=pr);
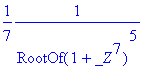
However, this does not work in the case of our
![]() .
.
> residue(f,x=p);
![]()
Another way this problem can arise is when you have a floating-point approximation to a singularity rather than an actual singularity.
> pf:= evalf(p);
![]()
> residue(f,x=pf);
![]()
In this case it's arguably not Maple's fault: the given point
![]() is not actually a singularity of
is not actually a singularity of
![]() , but only an approximation of a singularity. At
, but only an approximation of a singularity. At
![]() itself,
itself,
![]() has a finite (though large) value.
has a finite (though large) value.
> eval(f,x=pf);
![]()
If you know that
![]() should have a simple pole at the given point, you may be able to calculate the residue "by hand". For example:
should have a simple pole at the given point, you may be able to calculate the residue "by hand". For example:
> eval(numer(f)/diff(denom(f),x),x=p);
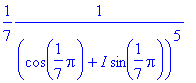
> eval(numer(f)/diff(denom(f),x),x=pf);
![]()
See also: convert[exp] , Exact vs floating-point computations , forget , Normalizer , residue , series , Testzero
Maple Advisor Database, R. Israel 2000