Description:
-
This procedure is an implementation of the functional calculus for matrices. It uses the undocumented procedure
`linalg/matfunc`
, which Maple itself seems to use only for exponentials.
-
If any of the entries of
A
include floating-point numbers, then all of its entries must be numerical.
-
If
f
is a function (e.g. a user-defined function such as
x -> x^2+1
or a named function such as
exp
), then
matfunc(A,f)
calculates
f(A)
. Any additional parameters to
matfunc
will then be used as additional parameters to
f
, e.g.
matfunc(A,f,p)
calculates
f(A,p)
. The function and whichever of its derivatives are needed must be defined at the eigenvalues of
A
.
-
If
f
is an expression, it must involve only one variable. If that variable is
t
,
matfunc(A,f)
calculates
g(A)
where
f = g(t)
.
-
matfunc
is based on the following definition of the functional calculus. Suppose the square matrix
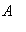 has eigenvalues
has eigenvalues
![lambda[j]](images/h25r2.gif) with algebraic multiplicities
with algebraic multiplicities
![m[j]](images/h25r3.gif) , and
, and
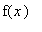 is defined and (if
is defined and (if
![m[j]](images/h25r5.gif) > 1)
> 1)
![m[j]-1](images/h25r6.gif) times differentiable at each lambda[j]. Then
times differentiable at each lambda[j]. Then
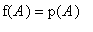 where
where
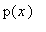 is a polynomial such that for each
is a polynomial such that for each
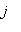 ,
,
![p(lambda[j]) = f(lambda[j])](images/h25r10.gif) and (if
and (if
![m[j]](images/h25r11.gif) > 1)
> 1)
![`@@`(D,k)(p)(lambda[j]) = `@@`(D,k)(f)(lambda[j])](images/h25r12.gif) for
for
![k <= m[j]-1](images/h25r13.gif) .
.
-
In particular,
matfunc
can be used (with
f = sqrt
) to compute a square root of the matrix
A
as long as 0 is not an eigenvalue of
A
with multiplicity greater than 1. This is not the most general case under which
A
has a square root, but it suffices for most purposes. In particular, if
A
is positive definite, the result will be the positive definite square root of
A
.
-
Another application (with
f = ln
) is finding a logarithm of a matrix, i.e. a matrix
B
such that
exp(B) = A
. This will work as long as
A
is nonsingular. Moreover, if
A
is positive definite
B
will be Hermitian (real and symmetric if
A
is real).
-
matfunc
is designed for symbolic exact computation. It may be used with matrices with floating-point entries, in which case the result will have floating-point entries, but these may not be very accurate unless a high setting of
Digits
is used.
-
If the characteristic polynomial of
A
is irreducible of degree 3 or higher, and
f
is not a polynomial, the results will be expressed as a sum over the roots of this polynomial (using
RootOf
). If it is reducible but some irreducible factor has degree 3 or higher,
matfunc
will return FAIL.
-
This function is part of the
Maple Advisor Database
library.
Examples:
>
A:= matrix([[11,3],[5,3]]);
![A := matrix([[11, 3], [5, 3]])](images/h25r14.gif)
Find a square root of
A
.
>
B:= matfunc(A,sqrt);
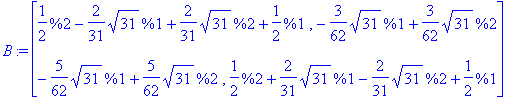
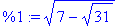
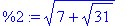
Check that it works:
>
map(normal,evalm(B^2));
![matrix([[11, 3], [5, 3]])](images/h25r18.gif)
Find a logarithm of
A
.
>
matfunc(A,ln);
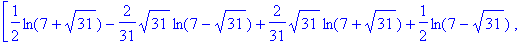
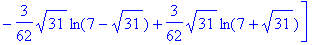
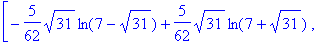
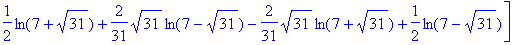
>
map(simplify,linalg[exponential](%));
![matrix([[11, 3], [5, 3]])](images/h25r23.gif)
A matrix whose characteristic polynomial is an irreducible quintic:
>
A:= linalg[companion](x^5 + x^4 -2* x^2 + 1,x);
![A := matrix([[0, 0, 0, 0, -1], [1, 0, 0, 0, 0], [0,...](images/h25r24.gif)
>
matfunc(A,sqrt);
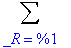
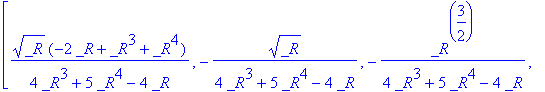
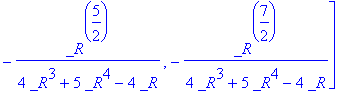
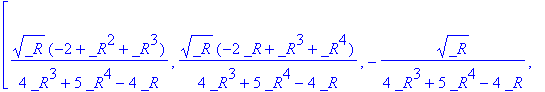
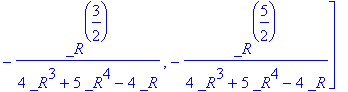
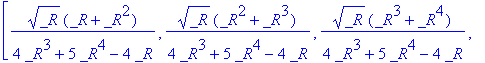
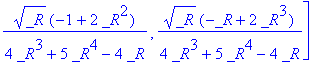
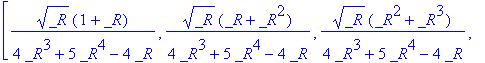
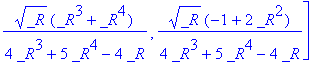
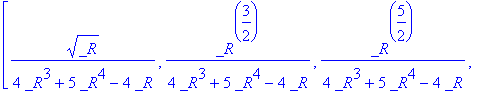
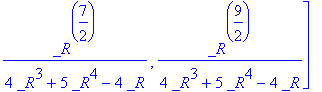
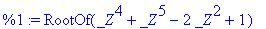
A floating-point example.
>
Af:= matrix([[0, 0, 36.], [1, 0, -49.], [0, 1, 14.]]);
![Af := matrix([[0, 0, 36.], [1, 0, -49.], [0, 1, 14....](images/h25r37.gif)
>
Bf:=matfunc(Af,sqrt);
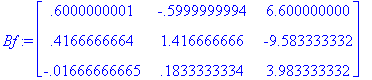
>
evalm(Bf^2);
![matrix([[.6e-9, .2e-8, 35.99999998], [.9999999990, ...](images/h25r39.gif)
![`@@`(D,k)(p)(lambda[j]) = `@@`(D,k)(f)(lambda[j])](images/h25r12.gif) for
for
![`@@`(D,k)(p)(lambda[j]) = `@@`(D,k)(f)(lambda[j])](images/h25r12.gif) for
for
![A := matrix([[11, 3], [5, 3]])](images/h25r14.gif)
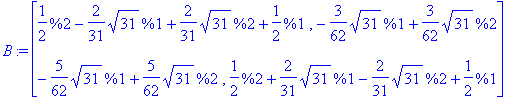
![]()
![]()
![matrix([[11, 3], [5, 3]])](images/h25r18.gif)
![]()
![]()
![]()
![]()
![matrix([[11, 3], [5, 3]])](images/h25r23.gif)
![A := matrix([[0, 0, 0, 0, -1], [1, 0, 0, 0, 0], [0,...](images/h25r24.gif)
![]()
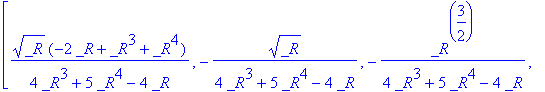
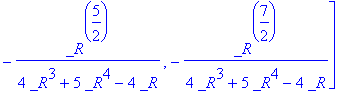
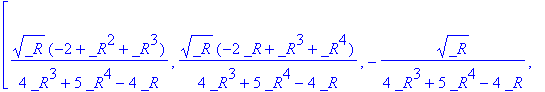
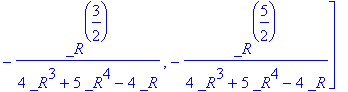
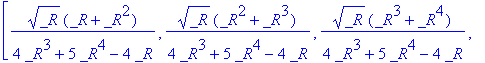
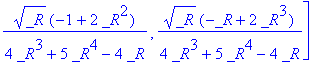
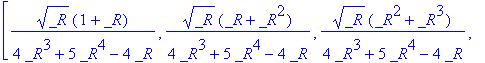
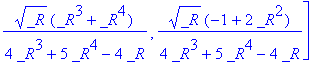
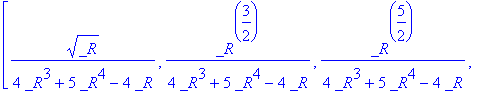
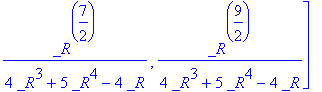
![]()
![Af := matrix([[0, 0, 36.], [1, 0, -49.], [0, 1, 14....](images/h25r37.gif)
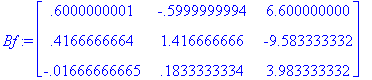
![matrix([[.6e-9, .2e-8, 35.99999998], [.9999999990, ...](images/h25r39.gif)