Function:
splitup - break up an integral, sum or product
Calling Sequence:
splitup(f, a);
splitup(f, a, vflag);
splitup(f, x = a);
splitup(f, x = a, vflag);
Parameters:
f
- an expression, usually containing at least one unevaluated definite integral, sum, or product
a
- a value for the dummy or index variable of the int, sum or product
x
- a dummy or index variable name (possibly indexed)
vflag
- (optional) true or false.
Description:
-
Splits up an integral, sum or product at the value
a
of the dummy variable, separating the values of the dummy variable
< a
and those
>= a
into separate integrals, sums or products. Thus
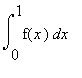 becomes
becomes
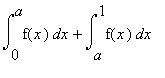 and
and
![Sum(f[i],i = m .. n)](images/h2r3.gif) becomes
becomes
![Sum(f[i],i = m .. a-1)+Sum(f[i],i = a .. n)](images/h2r4.gif) .
.
-
The inert forms
Int
,
Sum
,
Product
may be used instead of
int
,
sum
, or
product
to ensure that the integral, sum or product is not evaluated before being split.
-
If the variable name
x
is specified, only those integrals, sums or products with dummy variable named
x
will be split. Otherwise, for nested integrals, sums or products, the outermost one is split.
-
No splitting is done if it is known that the value
a
is outside the interval of the integral, sum or product. Note that the result is still valid even if
a
is outside the interval, according to the conventions Maple uses: e.g. for a sum, if
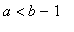 ,
,
![Sum(f[i],i = b .. a) = -Sum(f[i],i = a+1 .. b-1)](images/h2r6.gif) .
.
-
The value
a
need not be numeric, but in the case of a sum or product, if it is numeric it must be an integer.
-
For a sum or product, unless the optional third argument
vflag
is
false
, if in any of the results of the split the difference between the bounds is an integer, that part is evaluated explicitly (even though it is a
Sum
or
Product
). Thus if
![Sum(b[i],i = 1 .. n+1)](images/h2r7.gif) is split at
n
the result would be
is split at
n
the result would be
![Sum(b[i],i = 1 .. n-1)+b[n]+b[n+1]](images/h2r8.gif) . If
vflag
is
false
this would be
. If
vflag
is
false
this would be
![Sum(b[i],i = 1 .. n-1)+Sum(b[i],i = n .. n+1)](images/h2r9.gif) . In the case of
Int
, no evaluation is done. The non-inert forms
sum
,
product
and
int
will always attempt to evaluate.
. In the case of
Int
, no evaluation is done. The non-inert forms
sum
,
product
and
int
will always attempt to evaluate.
-
splitup
is automatically mapped into arrays, lists, sets, functions, +, * and ^.
-
This function is part of the Maple Advisor Database library.
Examples:
>
splitup(Int(f(x),x=a..c), b);
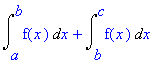
>
splitup(Sum(b[i], i=1 .. infinity) - Sum(b[i], i = 3 .. infinity), i = 3);
![b[1]+b[2]](images/h2r11.gif)
>
splitup(Sum(Product(c[i,j], i=k .. n), j = 1 .. m), i = p);
![Sum(Product(c[i,j],i = k .. p-1)*Product(c[i,j],i =...](images/h2r12.gif)
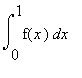 becomes
becomes
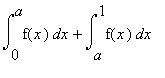 and
and
![Sum(f[i],i = m .. n)](images/h2r3.gif) becomes
becomes
![Sum(f[i],i = m .. a-1)+Sum(f[i],i = a .. n)](images/h2r4.gif) .
.
![Sum(f[i],i = b .. a) = -Sum(f[i],i = a+1 .. b-1)](images/h2r6.gif) .
.
![Sum(b[i],i = 1 .. n+1)](images/h2r7.gif) is split at
n
the result would be
is split at
n
the result would be
![Sum(b[i],i = 1 .. n-1)+b[n]+b[n+1]](images/h2r8.gif) . If
vflag
is
false
this would be
. If
vflag
is
false
this would be
![Sum(b[i],i = 1 .. n-1)+Sum(b[i],i = n .. n+1)](images/h2r9.gif) . In the case of
Int
, no evaluation is done. The non-inert forms
sum
,
product
and
int
will always attempt to evaluate.
. In the case of
Int
, no evaluation is done. The non-inert forms
sum
,
product
and
int
will always attempt to evaluate.
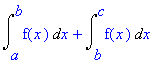
![Sum(Product(c[i,j],i = k .. p-1)*Product(c[i,j],i =...](images/h2r12.gif)