Function:
greatestroot - find floating-point approximation to greatest root of an equation or expression on a real interval.
Calling sequence:
greatestroot( expr, x = a .. b);
Parameters:
expr
- the equation or expression, involving one variable
x
- the variable (a name)
a, b
- endpoints of the interval (real constants).
Description:
-
greatestroot(expr, x=a..b)
computes numerically the greatest solution of an equation
expr
in one variable
x
in the real interval
a .. b
. If
expr
is an expression rather than an equation, the equation
expr = 0
is used. If there is no solution in this interval, nothing is returned.
-
Only one variable is allowed: the two sides of the equation must evaluate to real constants when any constant value in the interval
a .. b
is substituted for
x
.
-
The expression and all subexpressions should have at least two continuous derivatives on the interval. In particular, infinite limits at the endpoints, or indeterminate forms (such as
f/g
where
f
and
g
both approach
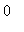 or
or
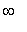 at the endpoints) may cause trouble.
at the endpoints) may cause trouble.
-
An exception to the requirements of continuity and differentiability is in the case of an expression defined piecewise, using
piecewise
,
signum
,
Heaviside
,
abs
,
min
or
max
, as long as
convert(...,pwlist)
can convert it to a list of expressions on different intervals. If this can't be done, an error occurs.
-
Infinite endpoints are allowed, but are not likely to work unless the expression has finite limits at those endpoints.
-
Since numerical techniques are used, the accuracy of the results is limited. In particular, a root of
f(x)
that is also a root of
D(f)(x)
may be computed with poor accuracy, or even missed entirely. In such a case it may be better to use
D(f)(x)
instead of
f(x)
. Increasing
Digits
should also improve accuracy.
-
In some difficult cases
greatestroot
may take a very long time. In particular, this will happen if the function is complicated or changes direction rapidly in the interval.
-
greatestroot
uses
evalr
to do interval arithmetic, and is therefore subject to the weaknesses of that procedure. In particular, it doesn't work with the two-variable version of
arctan
.
-
This function is part of the
Maple Advisor Database
library.
Examples:
>
greatestroot( tan(sin(x))=1, x = 0 .. 2*Pi );
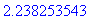
>
greatestroot((x-Pi)^2, x = 0 .. 4);
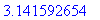
>
greatestroot(sin(x) + x^2, x = -infinity .. infinity);
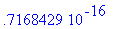
>
greatestroot(abs(sin(x)+x) = 1, x = -2 .. 2);
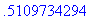
![]()
![]()
![]()
![]()