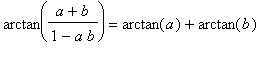 and
and
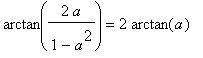 .
.
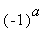 , while
expands(exp(I*a))
leaves it as
, while
expands(exp(I*a))
leaves it as
 .
.
Function: expands - symbolic version of expand
Calling sequences:
expands(expr);
Parameters:
expr - the expression to be expanded.
Description:
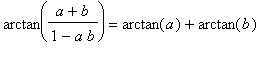 and
and
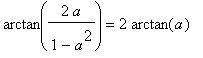 .
.
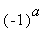 , while
expands(exp(I*a))
leaves it as
, while
expands(exp(I*a))
leaves it as
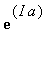 .
.
Examples:
Both expand and expands produce many of the same expansions.
> expands((x+1)*(x+2));
![]()
> expands(sin(x+y));
![]()
The expansion of the logarithm of a product. This is not always valid, as there may be an additional term
![]() where
where
![]() is an integer.
is an integer.
>
expand(ln(x*y)),expands(ln(x*y));
![]()
The square root of a product. This is not always valid, as there may be a factor of
![]() .
.
> expand(sqrt(x*y)),expands(sqrt(x*y));
![]()
A power of a power. Again, not always valid (e.g. try it for
![]() ).
).
> expand((x^(3/2))^(2/3)), expands((x^(3/2))^(2/3));
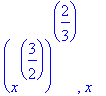
An expandable arctan. expand won't do anything with this, even under conditions that
guarantee its validity.
>
assume(x>0,x<1/4,y>0,y<1/4);
expand(arctan((x+y)/(1-x*y))), expands(arctan((x+y)/(1-x*y)));
![]()
A case where
expand
expands but
expands
does not. I think it is better to use
exp
rather than a power of
![]() here, to avoid complications with multivalued functions.
here, to avoid complications with multivalued functions.
> assume(x,real); expand(exp(2*Pi*I*x)), expands(exp(2*Pi*I*x));
![]()
See also:
assume , combine , expand
Maple Advisor Database R. Israel 2000