Shlomo Edward G. Belaga
C. N. R. S., Université Louis Pasteur
7, rue René Descartes
F-67084 STRASBOURG Cedex FRANCE
We present here a biblical exegesis of the value of ![]() ,
, ![]() , from the well known verse 1 Kings 7:23.
This verse is then compared to 2 Chronicles 4:2; the comparison
provides independent supporting evidence for the exegesis.
, from the well known verse 1 Kings 7:23.
This verse is then compared to 2 Chronicles 4:2; the comparison
provides independent supporting evidence for the exegesis.![[*]](foot.gif)
1.The Hebrew Bible often speaks the language of numbers and
measurements [Feldman 1965]; the Western tradition rarely![[*]](foot.gif) , if at all [Hoyrup
1989], understands this language, and the case of the Biblical value of
, if at all [Hoyrup
1989], understands this language, and the case of the Biblical value of
![]() could be seen as both a remarkable exception of this rule and its
striking confirmation.
could be seen as both a remarkable exception of this rule and its
striking confirmation.
As a recent publication in The American Mathematical Monthly
puts it, ``the ancient Hebrews regarded ![]() as being equal to
3'' [Almkvist, Berndt 1988, p. 599]. This claim (as several identical
claims made by both working mathematicians [Borwein, et al. 1989]
and historians of science [Bell 1945], [Beckmann 1971]) is based on the
plain meaning of the following verse of the Hebrew Bible, 1 Kings
7:23, giving the dimensions of a tank in the First
Temple
as being equal to
3'' [Almkvist, Berndt 1988, p. 599]. This claim (as several identical
claims made by both working mathematicians [Borwein, et al. 1989]
and historians of science [Bell 1945], [Beckmann 1971]) is based on the
plain meaning of the following verse of the Hebrew Bible, 1 Kings
7:23, giving the dimensions of a tank in the First
Temple![[*]](foot.gif) :
:
``And he made a molten sea [tank], ten cubits from the one brim to the other: it was round all about, and its height was five cubits: and a line of thirty cubits did circle it round about''. [Holy Scriptures, p. 412]
As a matter of fact, after mentioning this verse, people either can
not![[*]](foot.gif) , or do not want
, or do not want![[*]](foot.gif)
![[*]](foot.gif) , to hide (or are even happy for some
ideological reasons, to emphasize
, to hide (or are even happy for some
ideological reasons, to emphasize![[*]](foot.gif) ) their
surprise by such a low accuracy of the Biblical approximation,
) their
surprise by such a low accuracy of the Biblical approximation,
![]() , especially in the light of well-documented evidence that the
ancient Babylonians and Egyptians used for
, especially in the light of well-documented evidence that the
ancient Babylonians and Egyptians used for ![]() much better
approximations [Neugebauer 1969], [Gillings 1972] many hundred years
before this part of the Hebrew Bible was written:
much better
approximations [Neugebauer 1969], [Gillings 1972] many hundred years
before this part of the Hebrew Bible was written:
![]()
![]()
Thus, it seems both appropriate and interesting at this point to give a
Rabbinical interpretation of the above verse and the way the number
![]() , implicitly
, implicitly![[*]](foot.gif) defined in this verse, has to be
computed [Max Munk 1962 , 1968] (see also two popular and slightly
different accounts in [Posamentier, Gordan 1984] and [Roiter 1993]). We
do not claim, however, that the Rabbinical folklore has preserved either
the mathematical method which was used in this approximation of
defined in this verse, has to be
computed [Max Munk 1962 , 1968] (see also two popular and slightly
different accounts in [Posamentier, Gordan 1984] and [Roiter 1993]). We
do not claim, however, that the Rabbinical folklore has preserved either
the mathematical method which was used in this approximation of
![]() , or its historical origins: all that was left to us is an
extremely natural and concise mnemonic rule of the reconstruction of
, or its historical origins: all that was left to us is an
extremely natural and concise mnemonic rule of the reconstruction of
![]() (see more about it in [Max Munk 1962, 1968]).
(see more about it in [Max Munk 1962, 1968]).
Such an absence of mathematical justification is, of course, well known
to historians; as, e.g., a researcher writes about the value of
![]() : `` Just how this remarkably close approximation
was found, we do not know, but we can offer a suggestion on examining
the diagram of RMP 48'' (cited in [Gillings 1972, p. 142]). In our
case, no diagrams were preserved; one could even doubt that such
diagrams ever existed: ``ancient Hebrews'' have never regarded
mathematical or, for that matter, any other scientific knowledge
per se as deserving to be developed, preserved, and disseminated
in the written form, as they were not interested (with the Jewish Temple
being a notable exception) in creating numerous and splendid monuments
of their religion and culture.
: `` Just how this remarkably close approximation
was found, we do not know, but we can offer a suggestion on examining
the diagram of RMP 48'' (cited in [Gillings 1972, p. 142]). In our
case, no diagrams were preserved; one could even doubt that such
diagrams ever existed: ``ancient Hebrews'' have never regarded
mathematical or, for that matter, any other scientific knowledge
per se as deserving to be developed, preserved, and disseminated
in the written form, as they were not interested (with the Jewish Temple
being a notable exception) in creating numerous and splendid monuments
of their religion and culture.
2. The key to an alternative reading of the verse 1 Kings
7:23 is to be found in the very ancient Hebrew tradition (see, e.g.,
[Britannica 1985], [Banon 1987, pp. 52, 53]) to differently write
(spell) and read some words of the Bible; the reading
version is usually regarded as a correct one (in particular, it is
always correct from the point of view of the Hebrew grammar, and
this is why it could be easily either remembered or reconstructed from
the written version), whereas the written version slightly
deviates from the correct spelling. (Another approach, involving the
comparison between written forms of the same words in 1 Kings
7:23 and Chronicles 4:2 is cited in [Posamentiern, Gordan
1984]![[*]](foot.gif) ; see
more about this version of the exegesis in 4).
; see
more about this version of the exegesis in 4).
Such a disparity is a common feature for all Books of the Hebrew Bible; and in any such case there exists (or existed: some of this knowledge was definitely lost) a Rabbinical folklore (in fact, strict Rabbinical hermeneutical rules [Steinsaltz 1976, part three: Method], [Britannica 1985], [Banon 1987]) of interpretation of the difference in question.
In our case there is such a disparity for the word ``line'': in Hebrew, it is written as ``QVH (Qof, Vav, Hea)'', but it has to be read as ``QV (Qof, Vav)'' (the reader is advised to look at any edition of the Hebrew Bible with the Hebrew text and its translation; all disparities are either marked by an atersik, or the reading version is written on the margins).
Tradition asserts that not only does this disparity testify to an
approximate character of the given length of the line circling
around the ``sea''(tank), -- a much more accurate approximation to
![]() ,
, ![]() , is hidden in the choice of the written
version!
, is hidden in the choice of the written
version!
The letters of the Hebrew alphabets were traditionly used (well before
the building of the First Temple [Guitel 1975]) for numerical purposes
and, thus, have had numerical values ![[*]](foot.gif) .
Using these values, one can calculate values of words (as sums of values
of letters, but also in several other, less obvious and/or more involved
ways); these methods became later known as gematria [Michael Munk
1983, p. 163], [Britannica 1985]. Here are the standard numerical
equivalents of the letters of the Hebrew alphabet:
.
Using these values, one can calculate values of words (as sums of values
of letters, but also in several other, less obvious and/or more involved
ways); these methods became later known as gematria [Michael Munk
1983, p. 163], [Britannica 1985]. Here are the standard numerical
equivalents of the letters of the Hebrew alphabet:
In particular, the numerical equivalent of the written version ,``QVH'', is Qof+Vav+Hea=100+6+5=111, whereas the numerical equivalent of the reading version, ``QV'', is Qof+Vav=106.
Using these numerical equivalents, one defines ![]() as
follows:
as
follows:
![]()
![]()
![]()
3. Quantitatively, this is quite a remarkable approximation!
However, it is even more remarkable qualitatively. Here is a finite
section of the (infinite) continued fraction of the number ![]() :
:
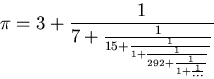
![]()
![]()
4. It is worthwhile to mention here a remarkable fact, namely, that in the case of the verse 1 Kings 7:23 we have an independent confirmation of the above mentioned written vs. reading disparity.
Namely, it could be easily seen that the verse 2 Chronicles 4:2 of the Hebrew Bible repeats 1 Kings 7:23 almost verbatim [Holy Scriptures, p. 988]. Looking at the Hebrew text, one immediately observes that the Hebrew word translated as line is traditionally spelled (written) here identically to its reading version. Thus, even if somebody would rebuff as irrelevant the problem of interpretation of the disparity written vs. reading version of the word line in 1 Kings 7:23 (because he does not trust the oral tradition of transmission of Biblical texts), he would still have to explain the disparity between two different written versions of the same word (with only one version being grammatically correct) in two almost identical verses of the Bible! This last disparity is chosen as the point of departure for the Rabbinical exegesis in [Posamentier, Gordan 1984].
One could ask, why would be this important hint to the enhanced value of
![]() omitted from the Books of Chronicles? An answer might be that the
Books of Chronicles were written more than four hundred years after the
Books of Kings, and the author of the Chronicles (traditionally
identified with the Scribe Ezra) was much more preoccupied with
rebuilding the Temple and preserving the spirit of the Torah, than with
the ``correct'' value of
omitted from the Books of Chronicles? An answer might be that the
Books of Chronicles were written more than four hundred years after the
Books of Kings, and the author of the Chronicles (traditionally
identified with the Scribe Ezra) was much more preoccupied with
rebuilding the Temple and preserving the spirit of the Torah, than with
the ``correct'' value of ![]() hidden in the descriptions of dimensions
of the sacred objects in the First Temple; still, Ezra has faithfully
reproduced these dimensions in his book.
hidden in the descriptions of dimensions
of the sacred objects in the First Temple; still, Ezra has faithfully
reproduced these dimensions in his book.
A methodological remark: whereas the exegesis based on comparison of written-vs.-reading versions of a verse is a very general method in the Rabbinical tradition [Munk 1962, 1968], [Banon 1987], the above exegesis exploits a more rare event: the existence of two almost identical verses.
5. The following question arising from the above analysis has to
be, at least briefly, touched upon: if the author of the first Book of
Kings (traditionally identified with Prophet Jeremiah) actually
knew the value ![]() and intentionally exploited the
aforementioned written-vs.-reading disparity to encode it, why
couldn't he simply write this value down in his text?
and intentionally exploited the
aforementioned written-vs.-reading disparity to encode it, why
couldn't he simply write this value down in his text?
The answer might be that the value ![]() , implicitly given in the
text, plays an important rôle as an approximation which was regarded
(and is still regarded) as best suited for all ritual purposes in
the everyday life of a common practitioner (possibly, mathematically
illiterate) of the Jewish law. Thus, our verse serves, in fact, (and so,
we conjecture, was it conceived by its author) as the [only]
textual basis for the following legal definition of
, implicitly given in the
text, plays an important rôle as an approximation which was regarded
(and is still regarded) as best suited for all ritual purposes in
the everyday life of a common practitioner (possibly, mathematically
illiterate) of the Jewish law. Thus, our verse serves, in fact, (and so,
we conjecture, was it conceived by its author) as the [only]
textual basis for the following legal definition of ![]() :
``Any [circle] which has a circumference of three fists has a diameter
of one fist'' [Mishnah 1983, p. 23] (this important dictum is
encountered in at least four different places of the Babylonian Talmud
[Max Munk 1962, 1968]).
:
``Any [circle] which has a circumference of three fists has a diameter
of one fist'' [Mishnah 1983, p. 23] (this important dictum is
encountered in at least four different places of the Babylonian Talmud
[Max Munk 1962, 1968]).
Still, all legal texts thoroughly investigate the problem [Max Munk
1962, 1968], [Scherman 1980], [Mishnah 1983, p. 22] and confirm that the
real value of ![]() is ``slightly bigger'' than 3, with some
commentators advancing an almost modern point of view on irrational
nature of
is ``slightly bigger'' than 3, with some
commentators advancing an almost modern point of view on irrational
nature of ![]() (the irrationality of
(the irrationality of ![]() was strictly proved only in
the late eighteenth century); thus, Rambam
was strictly proved only in
the late eighteenth century); thus, Rambam![[*]](foot.gif) comments:``...the [exact] ratio of the diameter of a
circle to its circumference cannot be known [is irrational]...but it is
possible to approximate it...and the approximation used by scientists
[Greeks and Arabs] is the ratio of one to three and one seventh...
Since it is impossible to arrive at a perfectly accurate ratio, ...
they [the Jewish Sages] assumed a round number and said: `Any [circle]
which has a circumference of three fists has a diameter of one fist'.
And they relied on this for all the measurements they needed'' [Mishnah
1983, p. 22].
comments:``...the [exact] ratio of the diameter of a
circle to its circumference cannot be known [is irrational]...but it is
possible to approximate it...and the approximation used by scientists
[Greeks and Arabs] is the ratio of one to three and one seventh...
Since it is impossible to arrive at a perfectly accurate ratio, ...
they [the Jewish Sages] assumed a round number and said: `Any [circle]
which has a circumference of three fists has a diameter of one fist'.
And they relied on this for all the measurements they needed'' [Mishnah
1983, p. 22].
It should be stressed that the purposed interpretation of the two-level
semantical structure of a Biblical verse (in our case, 1 Kings
7:23), one level for legal purposes, and another one for
``connoisseurs'', is not only a typical phenomenon in the Rabbinical
tradition -- in a sense -- such a multi-level approach to texts is the
main methodological legacy of this tradition [Steinsaltz 1976, Part
Three: Method], [Banon 87]. As Rabbi Moshe ben Nachman![[*]](foot.gif) writes: ``Everything that was transmitted to
Moses our teacher through the forty-nine gates of understanding was
written in the Torah explicitly or by implication in words, in the
numerical value of the letters or in the form of the letters, that is,
whether written normally or with some change in form, such as bent or
crooked letters, and other deviations...'' [Ramban 1971, Vol.1, p.
10].
writes: ``Everything that was transmitted to
Moses our teacher through the forty-nine gates of understanding was
written in the Torah explicitly or by implication in words, in the
numerical value of the letters or in the form of the letters, that is,
whether written normally or with some change in form, such as bent or
crooked letters, and other deviations...'' [Ramban 1971, Vol.1, p.
10].
Of course such an approach makes sense only if applied to texts which
are faithfully transmitted from generation to generation; in fact,
Judaism possesses elaborate institutions for such a
transmission![[*]](foot.gif) . In this
sense, it is (and always was) similar to modern science, with its
elaborated institutions of training and supporting professionals, whose
duty is to discover, accumulate, and transmit knowledge.
. In this
sense, it is (and always was) similar to modern science, with its
elaborated institutions of training and supporting professionals, whose
duty is to discover, accumulate, and transmit knowledge.
6. With all this understanding, gained thus far, we are, as yet, unable to elucidate the way the exegesis of the verse 1 Kings 7:23 has come to us: was it rediscovered by Rabbi Matityahu Hakohen Munk on his own [Max Munk 1962, 1968], or was it transmitted to him? Is there another source in the Rabbinical literature for the exegesis?
A formidable a priori difficulty in answering these and similiar
questions is related to unpleasant two thousand years old legacy of
Judaism: as a religion, it invariably remained during this period an
underdog, prone to persecutions and derision. This external pressure,
together with related to it scarcity of social resources, explain why
Rabbis have strictly separated legal matters (as, e.g., the legal
definition of ![]() ) from ``esoteric'' knowledge available to them
(our exegesis possibly included). In fact, it would be a nightmare
scenario for Rambam, or any other Jewish scholar who lived two
hundred years ago, or more, to advance a better approximation of
) from ``esoteric'' knowledge available to them
(our exegesis possibly included). In fact, it would be a nightmare
scenario for Rambam, or any other Jewish scholar who lived two
hundred years ago, or more, to advance a better approximation of ![]() , without being able (as we now are) to confirm this value
scientifically.
, without being able (as we now are) to confirm this value
scientifically.
This fundamental difficulty still remains the main obstacle to scientific ``customization'' of the vast body of esoteric knowledge accumulated, commented upon, and faithfully transmitted by Jewish scholars. The author hopes to be able to contribute more to our better understanding of this precious intellectual and spiritual heritage. cm Acknowledgements. Any acknowledgements would be both incomplete and difficult to appreciate without some rather personal remarks about the history of the writing of the present paper.
The author has acquired the knowledge of the Rabbinical exegesis of the verse 1 Kings 7:23 from Rabbi Haim Roth, of Mevasseret Yerushalaim, eleven years ago (the winter of 1979-1980); since then, several scholars in Talmudic studies have confirmed the existence of the exegesis, however, no sources for it were ever mentioned.
The author decided to publicize the exegesis, in the fall of 1990, after
he stumbled upon two recent papers in The American Mathematical
Monthly (written for a wide mathematical audience and devoted to new
methods of computation of ![]() ), which claimed, in a matter-of-fact
manner, that ``the ancient Hebrew regarded
), which claimed, in a matter-of-fact
manner, that ``the ancient Hebrew regarded ![]() as being equal to
3'', citing, of course, the verse 1 Kings 7:23 !
as being equal to
3'', citing, of course, the verse 1 Kings 7:23 !
The first draft of the paper appeared in October 1990, with a very
gratifying reponse from both the Talmudic and scientific communities.
The comments of Rabbi Naftali Gut, of Zürich, were most
inspiring. Rabbi Dr. Henri Biberfeld, Rabbis Daniel Mund and Arye Posen,
of Montréal, suggested several important Talmudic and Halachic
sources. Rabbi Dr. Nachum L. Rabinovich, of Maaleh Adumim, read
the paper and suggested an important correction. Discussions with Prof.
Louis Charbonneau, of Montréal, and his colleagues were
helpful in adjusting the presentation to the tastes of practitioners of
history of mathematics; the references [Feldman 1965], [Hoyrup 1989]
belong to Prof. Charbonneau. Later, he introduced the author to Prof.
Roger Herz-Fischler, of Carleton, to whom belongs the reference
[Zuidhof 1982]. Monsieur Luc Gagnon, the student of Prof. Jacques
Lefebvres, Montréal, supplied the reference [Posamentier, Gordan
1984]. Several manifestations of utmost disbelief (in few cases,
bordering on ridicule![[*]](foot.gif) ),
on the part of colleagues with, apparently, no previous exposure to
Jewish studies, helped the author to contain excitement and avoid
self-congratulation.
),
on the part of colleagues with, apparently, no previous exposure to
Jewish studies, helped the author to contain excitement and avoid
self-congratulation.
Finally, and miraculously, Prof. Edward Reingold, of Urbana, whose enthusiasm for the subject was most encouraging, introduced the author to Rabbi Dr. Zeharia Dor-Shav, of Bar-Ilan, who, by sheer coincidence, has just become aware about the existence of an exegesis and started to look for its source. In a week or so, the crucial references [Max Munk 1962, 1968] were found and transmitted to the author -- and all this has happened in the last week of April 1991, after eleven years of unsuccessful search for such a source! After hearing about the author's difficulties to locate the (Hebrew) references in Montréal, Prof. Reingold has found the articles in Urbana and sent the copies to the author.
Still, with all the aforementioned interest and encouragement, the risky endeavor to bridge the gap between the Rabbinical tradition and modern history of science would be impossible without the steadfastness and support of the author's family.
Note: The Rabbinical literature on the subject which are dealt with (or only briefly mentioned) in this paper is enormous. However, the present author has intentionally restricted his choice to such English (and, in three cases, French) references which are widely available in modern libraries. The only (and, unfortunately, unavoidable) exceptions are the original papers of Rabbi Max Munk, written in Hebrew and never translated in any of Western languages.
G. Almkvist, B. Bernd 1988: Gauss, Landen, Ramanujan,
the Arith- metic
-Geometric Mean, Ellipses, ![]() , and the Ladies Diary,
The Amer. Math. Monthly, 95, 585-608.
, and the Ladies Diary,
The Amer. Math. Monthly, 95, 585-608.
D. Banon 1987: La lecture infinie: Les voies de l'interprétation midra- chique, Éditions du Seuil, Paris.
P. Beckmann 1971: A History of ![]() (Pi), The Golem Press,
Boulder.
(Pi), The Golem Press,
Boulder.
E. T. Bell 1945: The Development of Mathematics, McGraw-Hill, New-York.
J. Brook 1988: The God of Isaac Newton, in: eds. J. Fauvel, et al., Let Newton Be!, Oxford Univ. Press, pp. 166-183.
J. M. Borwein, P. B. Borwein, D. H. Bailey 1989: Ramanujan, modular equations, and approximations to Pi, or How to compute one billion digits of Pi, The Amer. Math. Monthly, 96, 201-219.
Britannica (The New Encyclopedia) 1985, Vol. 14: Biblical literature and its critical interpretation, Vol 22: Judaism, Chicago.
W. M. Feldman 1965: Rabbinical Mathematics and Astronomy, Hermon Press, New-York.
R. J. Gillings 1972: Mathematics in the Time of the Pharaohs, The MIT Press, Cambridge.
G. Guitel 1975: Historie comparée des numérations écrites, Flammarion, Paris.
J. Hoyrup 1989: The Mathematical Context of the Bible, Technical
Report N![]() 2, university Centre, to appear in Anchor Bible
Dictionary.
2, university Centre, to appear in Anchor Bible
Dictionary.
The Holy Scriptures, Koren Publishers, Jerusalem, 1977.
A. Ya. Khintchine 1963: Continued Fractions, P. Noordhoff, Groningen.
F. Manuel 1974: The religion of Isaac Newton, Clarendon Press, Oxford.
Mishnah, The Artscroll Series, 1983: Seder Moed, Vol. 1(b): Eruvin, Mesorah Publications, New-York.
M(ax) Munk, Rabbi 1962: Three Geometry Problems in Tanach and Talmud (in Hebrew), SINAI (Mossad Harav Kook) 51 (5722) 218-227.
M(ax) Munk, Rabbi 1968: The Halachik Way for the Solution of Special Geometry Problems (in Hebrew), HADAROM (Rabbinical Council of America) 27 (5728) 115-133.
M(ichael) L. Munk, Rabbi 1983: The Wisdom in the Hebrew Alphabet, Mesorah, Brooklyn.
O. Neugebauer 1969: Vorlesungen über Geschichte der antiken mathematischen Wissenschaften, Erster Band: Vorgriechische Mathematik, Spring- er, Berlin.
A. S. Posamentier, N. Gordan 1984: An astounding revelation on the
history of ![]() , The Mathematics Teacher 77, N
, The Mathematics Teacher 77, N![]() 1,
pp. 52, 47.
1,
pp. 52, 47.
Ramban 1971: Commentary on the Torah, in five volumes. Translated by Rabbi Dr. C. B. Chavel, Shilo Publishing House, New-York.
H. Roiter 1993: La mer d'airain du Roi Salomon et le nombre ![]() (PI), Kountrass 7, N
(PI), Kountrass 7, N![]() 38, p. 10.
38, p. 10.
N. Scherman, Rabbi 1980: Measurements from Sinai, an overview to Bircas HaChammah, Mesorah Publications, New-York.
A. Steinsaltz 1976: The Essential Talmud, Basic Books, New-York.
R. S. Westfall 1987: Never at Rest, Cambridge Univ. Press, Cambridge.
Zuidhof 1982: King Solomon's molten sea and (![]() ), Biblical
Archeologist, Summer 1982, 179-184.
cm
), Biblical
Archeologist, Summer 1982, 179-184.
cm
