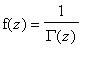 , where
, where
Let
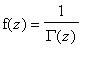 , where
, where
![]() is the gamma function, and let
is the gamma function, and let
![]() be the cubic polynomial that best approximates
be the cubic polynomial that best approximates
![]() on the unit disk in the supremum norm
on the unit disk in the supremum norm
![]() . What is
. What is
![]() ?
?
Solution:
Since the functions are analytic, the supremum will occur on the unit circle. So write f(z) and p(z) as functions of t where z = exp(I*t).
| > | restart; F:= t -> 1/GAMMA(exp(I*t)); F(Pi):= 0; |
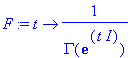
![]()
| > | P:= (a,t) -> a[0] + a[1]*exp(I*t)+ a[2]*exp(2*I*t)+a[3]*exp(3*I*t); |
![]()
Note that
![]() has the symmetry
has the symmetry
![]() . It is easy to show that the best approximation must have that symmetry too, which means we can assume the coefficients
. It is easy to show that the best approximation must have that symmetry too, which means we can assume the coefficients
![]() to
to
![]() are real. And then
are real. And then
![]() , so it suffices to take
, so it suffices to take
![]() in the interval
in the interval
![]() .
.
It's convenient to have the conjugates of these functions available.
| > | Fbar:= t -> 1/GAMMA(exp(-I*t));Fbar(Pi):= 0; |
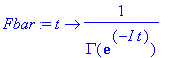
![]()
| > | Pbar:= (a,t) -> P(a,-t); |
![]()
We have to minimize with respect to
![]() the maximum with respect to
the maximum with respect to
![]() of
of
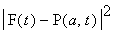 (this is a quadratic polynomial in
(this is a quadratic polynomial in
![]() ,...,
,...,
![]() , so it's a bit simpler to deal with than
, so it's a bit simpler to deal with than
![]() ). I can change this from a min-max question to a constrained minimization by writing it as
). I can change this from a min-max question to a constrained minimization by writing it as
minimize
![]() (with respect to
(with respect to
![]() and
and
![]() ) subject to
) subject to
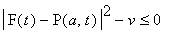 for each
for each
![]()
![]()
![]() .
.
Now write the Karush-Kuhn-Tucker conditions:
The Lagrangian is
![H(v,a,lambda) = v+sum((abs(F(t)-P(a,t))^2-v)*lambda[t],t)](images/challenge272.gif)
Formally the sum is over all
![]() . In general this might run into technical problems, but they won't occur here:
. In general this might run into technical problems, but they won't occur here:
![]() will be nonzero for only finitely many
will be nonzero for only finitely many
![]() . The Karush-Kuhn-Tucker conditions say
. The Karush-Kuhn-Tucker conditions say

![1-sum(lambda[t],t) = 0](images/challenge277.gif)
![diff(H(v,a,lambda),a[j]) = ``](images/challenge278.gif)
![sum(2*Re((P(a,-t)-F(-t))*exp(j*I*t))*lambda[t],t) = 0](images/challenge279.gif) for
for
![]()
![diff(H(v,a,lambda),lambda[t]) = ``](images/challenge281.gif)
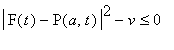 ,
,
![]() , and
, and
![lambda[t]*(abs(F(t)-P(a,t))^2-v) = 0](images/challenge284.gif) for
for
![]()
Note that this last condition implies
![]() for only finitely many
for only finitely many
![]() , since
, since
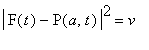 for only finitely many
for only finitely many
![]() .
.
Also, since the objective is linear and the constraints are convex, we don't have to worry about local minima. The Karush-Kuhn-Tucker conditions should have a unique solution, which will give us the global minimum.
Finding the solution is not so easy, however. I spent some time exploring the parameter space, looking for approximate solutions.
For a starting point, we can use a Taylor polynomial for f(z), corresponding to a partial sum of the Fourier series for F(t). This will give us the best approximation in the L^2 norm on the circle.
| > | ptayl:= taylor(1/GAMMA(z),z=0,4); |
![]()
| > | a0:= table([seq(j=evalf(coeff(ptayl,z,j)),j=0..3)]); |
![]()
| > | plot(abs(P(a0,t)-F(t))^2,t=0..Pi); |
![[Maple Plot]](images/challenge292.gif)
Here's a fast way to approximate the maximum of
![]() . Instead of all t, I'll just look at 90 of them.
. Instead of all t, I'll just look at 90 of them.
It's more convenient to use the list
![]() rather than the table
rather than the table
![]() (whose indices start at 0).
(whose indices start at 0).
| > | eits:= evalf([seq(exp(I*i*Pi/90),i=0..90)]): fvals:= evalf([seq(F(i*Pi/90),i=0..90)]): appnorm:= proc(L) local i; max(seq( abs(fvals[i]-L[1]-eits[i]*(L[2]+eits[i]*(L[3]+eits[i]*L[4]))),i=1..91)) end: |
Now we generate random steps from the current L, accepting the step if it improves the norm.
| > | ti:= time(): bestL:= [a0[0],a0[1],a0[2],a0[3]]: bestnorm:= appnorm(bestL); for iter from 1 to 5000 do L:= bestL + .01*exp(-.001*iter)*[stats[random,normald](4)]; newnorm:= appnorm(L); if newnorm < bestnorm then bestL:= L; bestnorm:= newnorm; print ("iteration",iter,bestnorm,L); else L:= 2*bestL-L; newnorm:= appnorm(L); if newnorm < bestnorm then bestL:= L; bestnorm:= newnorm; print ("iteration",iter,bestnorm,L); fi fi od: (time()-ti)*seconds; |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The last solution turns out to have 4 correct digits of the actual answer.
| > | a1:= table([seq(j=bestL[j+1],j=0..3)]); |
![]()
![]()
![]()
In our approximate solution,
![]() is close to constant from about
is close to constant from about
![]() to
to
![]() .
.
| > | plot(abs(F(t)-P(a1,t)),t=0..Pi); |
![[Maple Plot]](images/challenge356.gif)
On closer inspection, it achieves its maximum at three points in this interval, one of which is
![]() .
.
| > | plot(abs(F(t)-P(a1,t)),t=1..Pi,0.21 .. 0.21437 ); |
![[Maple Plot]](images/challenge358.gif)
| > | peak1:= fsolve(diff((F(t)-P(a1,t))*(Fbar(t)-Pbar(a1,t)),t), t= 1.4 .. 1.5); peak1:= simplify(%,zero); |
![]()
![]()
| > | peak2:= simplify(fsolve(diff((F(t)-P(a1,t))*(Fbar(t)-Pbar(a1,t)),t), t= 2.2 .. 2.3),zero); v1:= evalf(abs(F(Pi)-P(a1,Pi))^2); |
![]()
![]()
So we should expect
![]() for three values of
for three values of
![]() , say
, say
![]() ,
,
![]() and
and
![]() . We write the KKT equations with this assumption; note that in order to have
. We write the KKT equations with this assumption; note that in order to have
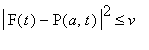 for all
for all
![]() and
and
![]() for
for
![]() we need
we need
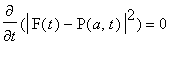 at
at
![]() . This is automatic at
. This is automatic at
![]() .
.
| > | t[3]:= Pi: kkt:= [ 1 - (lambda[1]+lambda[2]+lambda[3]), seq( add(((Pbar(a,t[i])-Fbar(t[i]))*exp(j*I*t[i])+(P(a,t[i])-F(t[i]))*exp(-j*I*t[i]))*lambda[i],i=1..3),j=0..3), seq( (F(t[i])-P(a,t[i]))*(Fbar(t[i])-Pbar(a,t[i])) - v, i=1..3), seq(eval(diff((F(t)-P(a,t))*(Fbar(t)-Pbar(a,t)),t), t=t[i]),i=1..2)]; |
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge375.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge376.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge377.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge378.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge379.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge380.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge381.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge382.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge383.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge384.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge385.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge386.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge387.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge388.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge389.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge390.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge391.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge392.gif)
![]()
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge394.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge395.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge396.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge397.gif)
![]()
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge399.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge400.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge401.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge402.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge403.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge404.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge405.gif)
![kkt := [1-lambda[1]-lambda[2]-lambda[3], (2*a[0]+a[1]*exp(-I*t[1])+a[2]*exp(-2*I*t[1])+a[3]*exp(-3*I*t[1])-1/GAMMA(exp(-I*t[1]))+a[1]*exp(t[1]*I)+a[2]*exp(2*I*t[1])+a[3]*exp(3*I*t[1])-1/GAMMA(exp(t[1]*...](images/challenge406.gif)
Here's what we have for these equations at our approximate solution.
| > | evalf(eval(kkt,{a=a1,t[1]=peak1, t[2]=peak2, v = v1})); |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | simplify(fnormal(%),zero); |
![]()
![]()
![]()
![]()
![]()
![]()
We need values for the Lagrange multipliers
![]() , from an overdetermined system with
, from an overdetermined system with
5 equations involving these.
| > | remove(type,%,constant); |
![]()
![]()
![]()
![]()
![]()
| > | lambdas:=linalg[leastsqrs](convert(%,set),{lambda[1],lambda[2],lambda[3]}); subs(lambdas,%%); |
![]()
![]()
Now using this approximate solution as a starting point, we solve the KKT equations using fsolve.
| > | approxsol:= lambdas union {seq(a[i]=a1[i],i=0..3),t[1]=peak1, t[2]=peak2, v = v1}; |
![]()
![]()
![]()
| > | Digits:= 30: fsolve(convert(kkt,set), approxsol); |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | sol:=simplify(fnormal(%),zero); |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
And the answer is:
| > | ans:= subs(sol,sqrt(v)); |
![]()
This is actually correct to 30 digits.