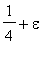 , and west with probability
, and west with probability
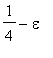 . The probability that the flea returns to (0,0) sometime during its wanderings is 1/2. What is
. The probability that the flea returns to (0,0) sometime during its wanderings is 1/2. What is
Problem 6:
A flea starts at (0,0) on the infinite 2D integer lattice and executes a biased random walk: At each step it hops north or south with probability 1/4, east with probability
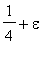 , and west with probability
, and west with probability
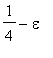 . The probability that the flea returns to (0,0) sometime during its wanderings is 1/2. What is
. The probability that the flea returns to (0,0) sometime during its wanderings is 1/2. What is
![]() ?
?
Solution:
If
![]() is the probability that the flea, starting at
is the probability that the flea, starting at
![]() , ever reaches (0,0), then
, ever reaches (0,0), then
![]() and otherwise
and otherwise
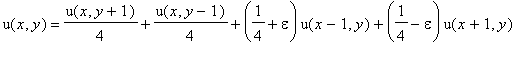 . The probability that the flea returns is
. The probability that the flea returns is
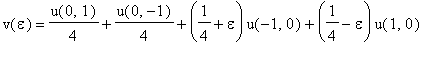 .
.
We can't calculate
![]() or
or
![]() directly, but we can approximate it by taking solving the equations in a finite region with boundary conditions
directly, but we can approximate it by taking solving the equations in a finite region with boundary conditions
![]() on the boundary of the region. This corresponds to looking at the situation where the flea is killed if it hits the boundary of the region. We want to find
on the boundary of the region. This corresponds to looking at the situation where the flea is killed if it hits the boundary of the region. We want to find
![]() (in this approximation) so that
(in this approximation) so that
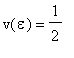 . This can be done by Newton's method: for this we need the derivatives of
. This can be done by Newton's method: for this we need the derivatives of
![]() and
and
![]() with respect to
with respect to
![]() , which satisfy the equations
, which satisfy the equations
obtained by differentiating the equations for u and v:
![]()
![]()
![]() otherwise
otherwise
![]()
![]()
I'll solve the system by iteration:
![]()
 = u[n](x,y+1)/4+u[n](x,y-1)/4+(1/4+epsilon)*u[n](x-1,y)+(1/4-epsilon)*u[n](x+1,y)](images/challenge484.gif)
I'll take advantage of the symmetry
![]() , and also the fact that (if you colour the
, and also the fact that (if you colour the
lattice as a checkerboard) the flea alternates between black and white sites, so we only
update, say, the black sites for odd n and the white ones for even n.
| > | getflea:= proc(eps,M) Procedure to do one Newton iteration for (2M+1) by (2M+1) grid local A,dA,i,j,iter,pp,pm,R,dR,Rp,ip,ip0,iip; u(x,y) = A[x+M,y+1] A:= hfarray(1..2*M,1..M); u'(x,y) = dA[x+M,y+1] dA:= hfarray(1..2*M,1..M); use R to check convergence by changes in u(1,0) R:= 0; Probabilities for east and west hops. pp:= 1/4+eps; pm:= 1/4-eps; Initialize the arrays for i from 1 to 2*M do for j from 1 to M do A[i,j]:= 0; dA[i,j]:= 0; od od: A[M,1]:= 1; ip =0 or 1 depending whether this iteration is for black or white sites if (-1)^M=1 then ip:= 0 else ip:= 1 fi; ip = ip0 on iterations that update u(1,0). ip0:= 1-ip; for iter from 1 do for each iteration ip:= 1-ip; update sites on y=0 for i from 2+ip to 2*M-1 by 2 do if i <> M then A[i,1]:= 0.5*A[i,2]+pp*A[i+1,1]+pm*A[i-1,1]; dA[i,1]:= 0.5*dA[i,2]+A[i+1,1]+pp*dA[i+1,1]-A[i-1,1]+pm*dA[i-1,1] fi od: iip:= ip; update sites not on y=0 for i from 2 to 2*M-1 do iip:= 1-iip; for j from 2+iip to M-1 by 2 do A[i,j]:= 0.25*(A[i,j-1]+A[i,j+1])+pp*A[i+1,j]+pm*A[i-1,j]; dA[i,j]:= 0.25*(dA[i,j-1]+dA[i,j+1])+pp*dA[i+1,j] +A[i+1,j]+pm*dA[i-1,j]-A[i-1,j]; od od; if ip=ip0 then Rp:= A[M+1,1]; if abs(Rp-R) <= 1e-15 then if no significant change in u(1,0), calculate v(eps) and next eps R:= pp*A[M+1,1]+pm*A[M-1,1]+0.5*A[M,2]; dR:= pp*dA[M+1,1]+A[M+1,1]+pm*dA[M-1,1]-A[M-1,1]+0.5*dA[M,2]; print(R,dR); return eps - (R-0.5)/dR; else R:= Rp; fi fi; od end; |
| > |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | Digits:= 15; ti:= time(): lasteps:= 0; eps:= 0.1: N:= 5: for iter from 1 while abs(lasteps - eps) > 1e-14 do N:= floor(3/2*N); lasteps:= eps: eps:= evalhf(getflea(eps,N)); (time()-ti)*seconds; od; |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The latest
![]() value of
value of
![]() should have more than 10 correct digits (actually it has 12, not counting the initial 0).
should have more than 10 correct digits (actually it has 12, not counting the initial 0).
But this method might be very slow if we wanted, say, 30 digits. Here's a different method that I thought of later, which works directly with the infinite lattice. First of all, according to probability theory, the probability
![]() of return is related to the expected number
of return is related to the expected number
![]() of times the flea is at (0,0) [including the first time] by
of times the flea is at (0,0) [including the first time] by

 . So we are looking for
. So we are looking for
![]() to make
to make
![]() . We can write this as the sum of the probabilities that the flea is at (0,0) at each time. Noting that this means making the same number of hops north as south and the same number east as west, we can write this as a convergent series
. We can write this as the sum of the probabilities that the flea is at (0,0) at each time. Noting that this means making the same number of hops north as south and the same number east as west, we can write this as a convergent series

![`` = sum(c[j]*q^j,j = 0 .. infinity)](images/challenge581.gif) where
where
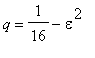 . All we need to do is compute the coefficients
. All we need to do is compute the coefficients
![]() , sum the series and solve for
, sum the series and solve for
![]() . The series doesn't converge very quickly: the radius of convergence is 1/16 (since
. The series doesn't converge very quickly: the radius of convergence is 1/16 (since
![]() for
for
![]() , i.e.
, i.e.
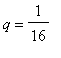 ), and we will be looking at values of q rather close to 1/16. So we'll need lots of terms to get an accurate value.
), and we will be looking at values of q rather close to 1/16. So we'll need lots of terms to get an accurate value.
Maple calculates c[j] as an expression involving a hypergeometric function. Maple 8 can convert this to an expression involving associated Legendre functions.
| > | cj:= sum((2*j+2*k)!/(j!)^2/(k!)^2*(1/4)^(2*k),k=0..infinity) assuming j::posint; |
![cj := (2*j)!/j!^2*hypergeom([j+1, j+1/2],[1],1/4)](images/challenge588.gif)
| > | convert(%,`2F1`); # Maple 8 required |

We want to calculate
![]() numerically, which Maple can do quite nicely for each
numerically, which Maple can do quite nicely for each
![]() using the hypergeom expression. If we want, say, about 30 digits, we'll want enough terms until
using the hypergeom expression. If we want, say, about 30 digits, we'll want enough terms until
![c[j]*q^j < 10^(-31)](images/challenge592.gif) for the
for the
![]() we'll be using. I'll do the calculations with 40 digits.
we'll be using. I'll do the calculations with 40 digits.
| > | Digits:= 40: ti:= time(): q0:= 1/16 - .06^2: for j from 0 do c[j]:= evalf(cj); if c[j]*q0^j < 1e-31 then break fi; od: (time()-ti)*seconds; |
![]()
| > | j; |
![]()
| > | c[j]*q0^j; |
![]()
| > | Newt:= proc(eps) local q,j,v,vp; This does one iteration of Newton's method for ![sum(c[j]*q^j,j = 1 .. 1067) = 2](images/challenge597.gif)
q:= evalf(1/16 - eps^2); v:= add(c[j]*[1,j/q]*q^j,j=0..1067); q:= q - (v[1]-2)/v[2]; sqrt(1/16-q); end; |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | epsilon:= 0.06; ti:= time(): do oldepsilon:= epsilon: epsilon:= Newt(epsilon); print(epsilon); if abs(oldepsilon-epsilon) < 1e-30 then break fi; od: (time()-ti)*seconds; |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
This has 31 correct digits.