Problem 8:
A square plate
![]() x
x
![]() is at temperature
is at temperature
![]() . At time
. At time
![]() the temperature is increased to
the temperature is increased to
![]() along one of the four sides while being held at
along one of the four sides while being held at
![]() along the other three sides, and heat then flows into the plate according to
along the other three sides, and heat then flows into the plate according to
![]() . When does the temperature reach
. When does the temperature reach
![]() at the center of the plate?
at the center of the plate?
Solution:
This is a standard heat-equation problem with homogeneous boundary conditions. It will be slightly more convenient to take the plate as [0,2] x [0,2], and the side with
![]() will be taken as
will be taken as
![]() . The solution is obtained as the sum of a steady-state solution v
. The solution is obtained as the sum of a steady-state solution v
![(x, y) = sum(a[j]*sinh(j*Pi*x/2)*sin(j*Pi*y/2),j = 1 .. infinity)](images/challenge657.gif) with
with
![a[j] = int(5/sinh(j*Pi)*sin(j*Pi*y/2),y = 0 .. 2)](images/challenge658.gif) so that
so that
![]() , and a solution of the equation with homogeneous boundary conditions,
, and a solution of the equation with homogeneous boundary conditions,
![w(x,y,t) = sum(sum(b[i,j]*sin(i*Pi*x/2)*sin(j*Pi*y/2)*exp(-Pi^2*(i^2+j^2)/4*t),i = 1 .. infinity),j = 1 .. infinity)](images/challenge660.gif) with
with
![b[i,j] = -a[j]*int(sin(i*Pi*x/2)*sinh(j*Pi*x/2),x = 0 .. 2)](images/challenge661.gif) so that
so that
![]() .
.
| > | aj:= int(5/sinh(j*Pi)*sin(j*Pi*y/2),y = 0 .. 2) assuming j::posint; |
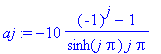
| > | bij:= -aj*int(sin(i*Pi*x/2)*sinh(j*Pi*x/2),x = 0 .. 2) assuming i::posint,j::posint; |
![]()
![]()
![]()
| > | bij:= simplify(evalc(convert(%,exp))) assuming i::posint,j::posint; |
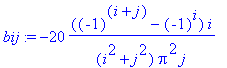
We want to evaluate this at x=1, y=1. By symmetry it is obvious that v(1,1) = 5/4.
As for
![]() , the factor
, the factor
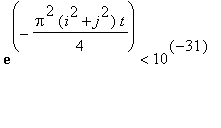 for
for
 (some preliminary investigation assured us that the answer we want should be somewhere between about 1/4 and 1) if
(some preliminary investigation assured us that the answer we want should be somewhere between about 1/4 and 1) if
 . So this approximation to
. So this approximation to
![]() should be accurate to approximately 30 decimals when
should be accurate to approximately 30 decimals when
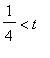 :
:
| > | U:= 5/4 + add(add(bij*sin(i*Pi*1/2)*sin(j*Pi*1/2)*exp(-Pi^2*(i^2+j^2)/4*t),j=1..floor(sqrt(116-i^2))),i=1..10); |
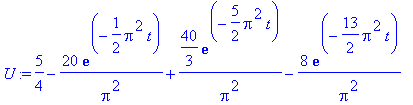
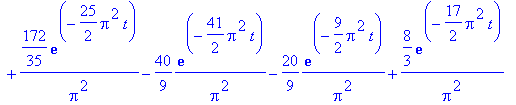
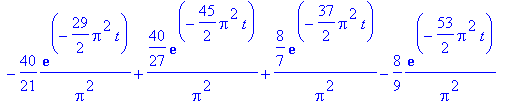
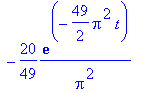
Now to solve
![]() :
:
| > | Digits:= 40: fsolve(U=1,t=1/4 .. 1); |
![]()
This actually has 39 correct digits.