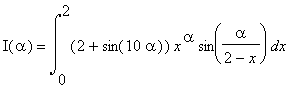 depends on the parameter
depends on the parameter
Problem 9:
The integral
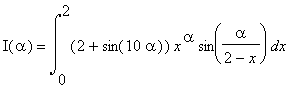 depends on the parameter
depends on the parameter
![]() . What is the value
. What is the value
![]() at which
at which
![]() achieves its maximum?
achieves its maximum?
This is rather different from Gaston's solution. The numerical integration works in Maple 8, but not Maple 7.
We want to be able to evaluate
![]() and
and
![]() so that we can use Newton's method to find the location of the maximum. Write
so that we can use Newton's method to find the location of the maximum. Write
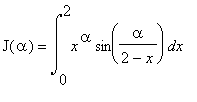 so
so
![]() ,
,
![]() , and
, and
![]() .
.
We break the interval up into pieces.
On the interval
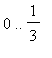 we use a series in powers of
we use a series in powers of
![]() . On
. On
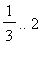 we use the transformation
we use the transformation
 , obtaining an integral on
, obtaining an integral on
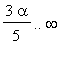 . On the interval
. On the interval
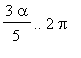 we use Maple's own numerical integration, and on
we use Maple's own numerical integration, and on
![]() we expand the integrand in negative powers of y times sin(y).
we expand the integrand in negative powers of y times sin(y).
| > | restart: ti:= time(): |
First for the interval
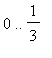 : J1 is the integral, dJ1 its derivative and d2J1 its second derivative.
: J1 is the integral, dJ1 its derivative and d2J1 its second derivative.
| > | f:= x^alpha*sin(alpha/(2-x)); S:= convert(series(sin(alpha/(2-x)),x,40),polynom): intp:= proc(t) local c,xp,n; if has(t,x) then xp,c := selectremove(has,t,x); if xp = x then n:= 1 else n:= op(2,xp) fi; else n:= 0; c:= t fi; collect(expand(c),[cos,sin])*3^(-n-alpha-1)/(n+alpha+1); end: J1:= map(intp,S): |
![]()
| > | dJ1:= diff(J1,alpha): d2J1:= diff(J1,alpha$2): |
| > | length(J1),length(dJ1),length(d2J1); |
![]()
How big is the last term in dJ1 for a typical alpha?
| > | evalf(eval(select(has,dJ1,3^(-40-alpha)),alpha=0.8)); |
![]()
Next the transformation.
| > | xy := expand(solve(alpha/(2-x)=y,x)); g:= subs(x=xy,f)*diff(xy,y); g1:= eval(g,y=3*alpha/5); ga:= normal(diff(g,alpha)); ga1:= normal(eval(ga,y=3*alpha/5)); gy:= normal(eval(diff(g,y),y=3*alpha/5)); gaa:= normal(diff(g,alpha$2)); |
![]()
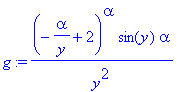
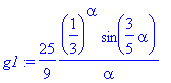

![]()
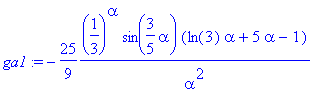
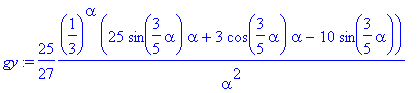
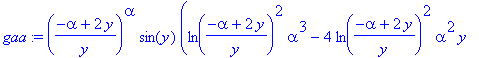
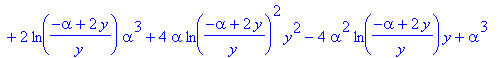
![]()
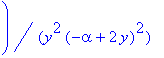
So we want
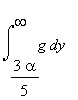 .
.
![]() is the integral from
is the integral from
![]() to
to
![]() ,
,
![]() and
and
![]() its derivatives. Maple sometimes seems to have trouble evaluating
its derivatives. Maple sometimes seems to have trouble evaluating
![]() to high precision, but we don't need as much accuracy there, so the relative error tolerance
to high precision, but we don't need as much accuracy there, so the relative error tolerance
![]() can be increased in this case.
can be increased in this case.
| > | dH:=diff(int(h(a,y),y=3*a/5 .. 2*Pi),a); d2H:=diff(int(h(a,y),y=3*a/5 .. 2*Pi),a$2); |
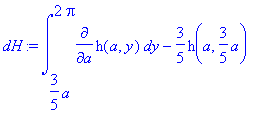
![]()
(a,3/5*a)-9/25*D[2](h)(a,3/5*a)](images/challenge722.gif)
| > | J2:= a -> evalf(Int(subs(alpha=a,g),y=3*a/5 .. 2*Pi)); |
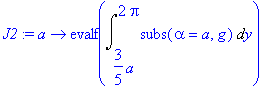
| > | dJ2:= a -> evalf(Int(subs(alpha=a,ga),y=3*a/5 .. 2*Pi) - 3/5*subs(alpha=a,g1)); d2J2:= a -> evalf(Int(subs(alpha=a,gaa),y=3*a/5 .. 2*Pi,epsilon=10^(-Digits/2)) - subs(alpha=a,6/5*ga1+9/25*gy)); |

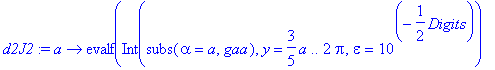
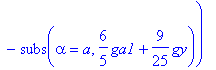
| > | J2(0.8),dJ2(0.8),d2J2(0.8); |
![]()
For the interval
![]() , we will use a series for
, we will use a series for
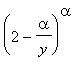 in negative powers of
in negative powers of
![]() , relying on Maple to integrate
, relying on Maple to integrate
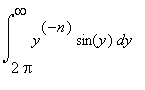 . We have
. We have
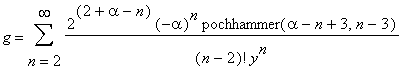 where
where
![]() .
.
| > | J3:=add(2^(2+alpha-n)*(-alpha)^n*pochhammer(alpha-n+3,n-3)/(n-2)!*int(sin(y)/y^n,y=2*Pi..infinity),n = 2 .. 30): |
| > | dJ3:= diff(J3,alpha): d2J3:= diff(J3,alpha$2): |
| > | evalf(eval([J3,dJ3,d2J3],alpha=0.8)); |
![]()
| > | t30:= add(2^(2+alpha-n)*(-alpha)^n*pochhammer(alpha-n+3,n-3)/(n-2)!*int(sin(y)/y^n,y=2*Pi..infinity),n = 30..30); evalf(eval([t30,diff(t30,alpha),diff(t30,alpha$2)],alpha=0.8)); |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | Jp:= a -> evalf(eval(J1+J3,alpha=a))+J2(a): Ip:= a -> evalf(2+sin(10*a))*Jp(a): Jp(0.8); |
![]()
Here it is plotted (with low precision),
![]() in red and
in red and
![]() in green. The maximum is near
in green. The maximum is near
![]() .
.
| > | plot([Jp,Ip],0..5); |
![[Maple Plot]](images/challenge750.gif)
Here is a Newton iteration procedure. It takes an initial
![]() value, prints the values of
value, prints the values of
![]() ,
,
![]() and
and
![]() , and returns the new alpha for the next iteration:
, and returns the new alpha for the next iteration:
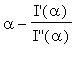 .
.
| > | Newt:= proc(a) local J,dJ,d2J,Ia,dI,d2I; J:= evalf(eval(J1+J3,alpha=a)+J2(a)); dJ:= evalf(eval(dJ1+dJ3,alpha=a)+dJ2(a)); d2J:= evalf(eval(d2J1+d2J3,alpha=a)+d2J2(a)); Ia:= (2+sin(10*a))*J; dI:=10*cos(10*a)*J+(2+sin(10*a))*dJ; d2I:= -100*sin(10*a)*J+20*cos(10*a)*dJ+(2+sin(10*a))*d2J; print([Ia,dI,d2I]); a-dI/d2I; end; |
| > |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
| > | a1:=Newt(0.8); |
![]()
![]()
| > | Digits:= 36: for i from 2 to 5 do a||i:= Newt(a||(i-1)) od; (time()-ti)*seconds; |
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
This has 33 correct digits.
| > |