O and Order

The ``Big-Oh'' notation is convenient for describing errors. If $f$ and $g$ are functions defined for small positive values of $h$, we write $f = O(g)$ to mean that there are positive constants $K$ and $\delta$ such that

$$\vert f(h)\vert \le K \vert g(h)\vert \quad {\rm when}\quad 0 < h < \delta$$

In other words, when $h$ is small and positive, $\vert f\vert$ is bounded by some constant times $\vert g\vert$. Typically, we use some power of $h$ for $g$. If $f = O(h^p)$ we say that ``$f$ is of order $h^p$'' or sometimes ``$f$ is of $p$'th order in $h$''. The symbol $O(h^p)$ can often be thought of as standing for ``terms of order $h^p$''. For example, from the Taylor series we have $$\exp(h) = 1 + h + h^2/2 + O(h^3)$$. In general, if $f(h)$ can be represented as a convergent Taylor series $$a_0 + a_1 h + a_2 h^2 + ...$$ (at least when $h$ is small) we can say

$$f(h) = a_0 + a_1 h + ... + a_{p-1} h^{p-1} + O(h^p)$$

for any positive integer $p$.

Since we don't care what the constant $K$ is, we can write ``equations'' such as $O(h) O(h^2) = O(h^3)$. This is shorthand for the following: We have one function $f(h) = O(h)$, i.e. $\vert f(h)\vert < K_1 h$ when $h$ is small, and another function $g(h) = O(h^2)$, i.e. $\vert g(h)\vert < K_2 h^2$ when $h$ is small. Then $f(h) g(h) = O(h^3)$, since $\vert f(h) g(h)\vert < K_1 K_2 h^3$ when $h$ is small.

Typically our $f(h)$ will represent an error, which of course we want to be as small as possible. The way we could make it small is to use a small $h$. Generally, we might expect a higher order approximation to be better than a lower order one. This is certainly true ``eventually'', i.e. for sufficiently small values of $h$. However, it's not necessarily true for any particular value of $h$. For example, if $f(h) = O(h)$ and $g(h) = O(h^2)$, then we might expect $g(h) < f(h)$ when $h$ is small. But we might have, say, $f(h) = h$ and $$g(h) = 10^{10} h^2$$. It's true that $g(h) < f(h)$ when $h$ is ``small'', but in this case ``small'' means $h < 10^{-10}$.

Consider the approximation of $\exp(x)$ by $$Q(h) = (1 + x h)^{1/h}$$. This has a Taylor series about $h = 0$ (where we define $Q(0) = \exp(x)$). The easy way to obtain the first few terms of the series is by writing $Q(h) = \exp(\ln(1+xh)/h)$: the Taylor series for $\ln(1+xh)$ about $h = 0$ starts $xh - x^2 h^2/2 + ...$, so

$$\frac{\ln(1+xh)}{h} = x - \frac{x^2}{2} h + O(h^2)$$

$$\exp\left(\frac{\ln(1+xh)}{h}\right) = {\rm e}^x \exp\left( ... ...2)\right) = {\rm e}^x \left(1 - \frac{x^2}{2} h + O(h^2)\right)$$

$$= {\rm e}^x - {\rm e}^x \frac{x^2}{2} h + O(h^2)$$

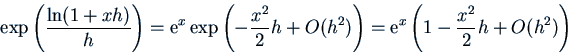
The error in the approximation is

$$E(h) = {\rm e}^x - Q(h) = {\rm e}^x \frac{x^2}{2} h + O(h^2)$$

If we don't care what the coefficient of $h$ is, we could also say the error is $O(h)$.

Here is a graph showing the error $E(h)$ as a function of $h$ in the case $x = 1$, using some 34 different values of $h$ from $1/500$ to $1/10$:

<img src="bigoh.gif">