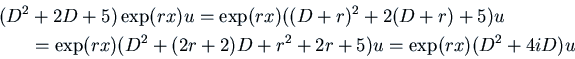Example: Solve
![]() .
.
The characteristic equation
![]() has roots
has roots
![]() so we have a fundamental set of solutions:
so we have a fundamental set of solutions:
![]() and
and
![]() . Note that the two complex roots are complex conjugates of
each other, and also the corresponding solutions of the
differential equation are complex conjugates of each other.
. Note that the two complex roots are complex conjugates of
each other, and also the corresponding solutions of the
differential equation are complex conjugates of each other.
Now usually we expect our solutions to differential equations to be real.
Certainly if ![]() is supposed to represent some real physical quantity, we
would be interested in a real solution. Real solutions can be obtained
as suitable linear combinations of our fundamental set of
complex solutions. For example,
is supposed to represent some real physical quantity, we
would be interested in a real solution. Real solutions can be obtained
as suitable linear combinations of our fundamental set of
complex solutions. For example,
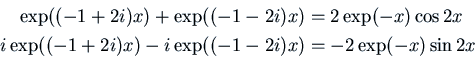
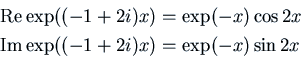
|
Let |
In particular, this says that if ![]() is a complex root of the real polynomial
is a complex root of the real polynomial
![]() then
then
![]() and
and
![]() are solutions of
the homogeneous equation
are solutions of
the homogeneous equation
![]() . If
. If ![]() , these
solutions are
, these
solutions are
![]() and
and
![]() .
.
There is no need, however, to restrict ourselves to homogeneous equations.
Example: Find a particular solution of
![]() .
.
The right side is
the real part of
![]() . So we can solve
. So we can solve
![]() , and then take
, and then take
![]() . Now for
. Now for
![]() we have
we have
![]() , so
, so
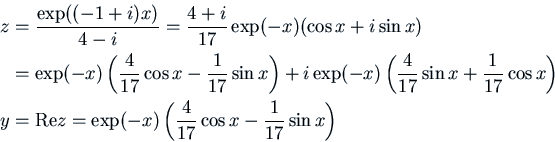
We can also use this principle together with the Exponential Shift Theorem.
Example: Find a particular solution of
![]() .
.
Let ![]() .
We want to find a particular solution of
.
We want to find a particular solution of
![]() and then take
and then take
![]() .
Since
.
Since
![]() , we must take
, we must take
![]() .
According to the Exponential Shift Theorem,
.
According to the Exponential Shift Theorem,