We begin with the undamped case:
Undamped Forced Vibrations
We begin with the undamped case: ![]() . As we have done in the
Constant Coefficients: Complex Roots page, we look for a
particular solution of the form
. As we have done in the
Constant Coefficients: Complex Roots page, we look for a
particular solution of the form
![]() where
where
![]() . Moreover, for that equation we would
take a trial solution
. Moreover, for that equation we would
take a trial solution
![]() (in the case where
(in the case where ![]() is not a root of the characteristic equation, i.e.
is not a root of the characteristic equation, i.e.
![]() ).
We get
).
We get
![]() where
where
![]() is the natural angular frequency of the spring-mass system
(i.e. the homogeneous system has solutions with angular frequency
is the natural angular frequency of the spring-mass system
(i.e. the homogeneous system has solutions with angular frequency ![]() ).
Thus our particular solution is
).
Thus our particular solution is
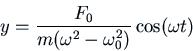
When
![]() , i.e.
the natural frequency of the system is higher than the frequency of the external
force, we find that
, i.e.
the natural frequency of the system is higher than the frequency of the external
force, we find that ![]() is in phase with the external force. Here is a picture
of this: the external force is provided by moving the support of the spring
up and down (the top curve), and the response
is in phase with the external force. Here is a picture
of this: the external force is provided by moving the support of the spring
up and down (the top curve), and the response ![]() is the bottom curve.
In this case
is the bottom curve.
In this case
![]() and
and ![]() . Note that the mass
is up when the support is up, and down when the support is down.
. Note that the mass
is up when the support is up, and down when the support is down.
 Click on picture for animation.
Click on picture for animation.
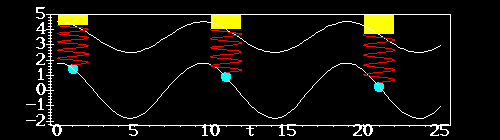
On the other hand, when
![]() , i.e. the natural frequency
is lower than the frequency of the external force, the coefficient of
, i.e. the natural frequency
is lower than the frequency of the external force, the coefficient of
![]() is negative, which means that
is negative, which means that ![]() is 180 degrees out
of phase with the external force. Here is a picture of this, with
is 180 degrees out
of phase with the external force. Here is a picture of this, with
![]() and
and ![]() .
Note that the mass
is down when the support is up, and up when the support is down.
.
Note that the mass
is down when the support is up, and up when the support is down.
 Click on picture for animation.
Click on picture for animation.
Of course, this is only one particular solution. For the general solution,
we must add the general solution of the homogeneous equation, obtaining
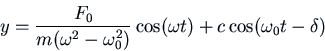
For example, consider the initial conditions ![]() ,
,
![]() . A solution satisfying these initial conditions is
. A solution satisfying these initial conditions is
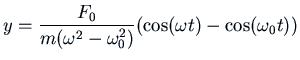 . We can rewrite this using a trigonometric identity:
. We can rewrite this using a trigonometric identity:
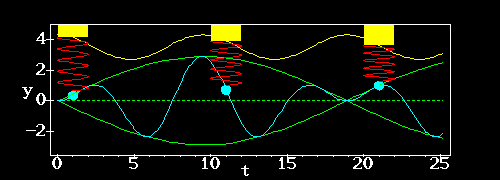 Click on picture for animation
Click on picture for animation
The effect is that of an angular frequency that is the average of
![]() and
and ![]() , with an amplitude that varies because of the
low-frequency factor
, with an amplitude that varies because of the
low-frequency factor
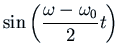 . This phenomenon is known as ``beats'': in an audio signal
you hear the signal grow louder and softer, dying out when
. This phenomenon is known as ``beats'': in an audio signal
you hear the signal grow louder and softer, dying out when
![]() is a multiple of
is a multiple of ![]() and sounding loudest when it is an
odd multiple of
and sounding loudest when it is an
odd multiple of ![]() . This can be used to tune stringed instruments
such as guitars.
. This can be used to tune stringed instruments
such as guitars.
Resonance
Our formula for the particular solution doesn't work in the case
![]() , for which we would have
, for which we would have ![]() in the denominator.
Instead, our methods for ``Case 2'' tell us to take a trial solution
for
in the denominator.
Instead, our methods for ``Case 2'' tell us to take a trial solution
for
![]() of the form
of the form
![]() . We then get
. We then get
![]() so
our particular solution is
so
our particular solution is
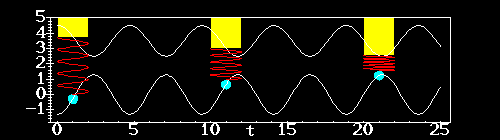
The picture shows our spring-mass system, starting from rest, with the support moving up and down at the resonant frequency with amplitude 0.2. Eventually the mass collides with the support of the spring.
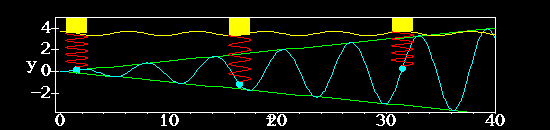 Click on picture for animation.
Click on picture for animation.
Damped Forced Vibrations
Now suppose the damping constant ![]() is positive.
Again we take
is positive.
Again we take
![]() with
with
![]() , and use a trial solution
, and use a trial solution
![]() . This should work since the roots of the
characteristic equation will all have negative real parts. We get
. This should work since the roots of the
characteristic equation will all have negative real parts. We get
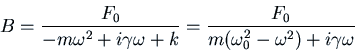
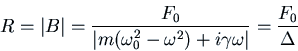
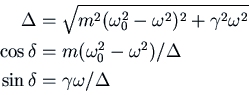
For example, if ![]() ,
, ![]() and
and ![]() , we have
, we have
![]() . Suppose
. Suppose ![]() and
and
![]() .
We get
.
We get
![]() so
so ![]() ,
,
![]() ,
,
![]() so
so
![]() .
.
Again, this is one particular solution. It is called the steady-state
solution, because it represents a vibration with constant amplitude.
A solution of
the homogeneous equation, which we add to get any other solution, is
called a transient: because of the damping, these contain a factor
![]() and go to 0 as
and go to 0 as ![]() . Thus whatever
initial conditions you start with, if you wait long enough the solution
will be very close to the steady state solution.
. Thus whatever
initial conditions you start with, if you wait long enough the solution
will be very close to the steady state solution.
In our example, which is underdamped,
![]() and
and
![]() .
Consider the initial conditions
.
Consider the initial conditions
![]() . The steady-state
solution has
. The steady-state
solution has
![]() and
and
![]() , so the
transient will have
, so the
transient will have ![]() and
and
![]() .
The transient is
.
The transient is
![]() . Here is the solution:
. Here is the solution:
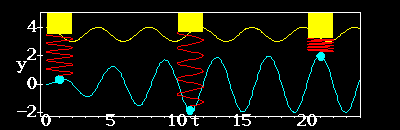 Click on picture for animation.
Click on picture for animation.
The above example had
![]() , which in an undamped
system would result in
, which in an undamped
system would result in ![]() being 180 degrees or
being 180 degrees or ![]() radians
out of phase with the external force. With damping,
if
radians
out of phase with the external force. With damping,
if
![]() we will have
we will have
![]() and
and
![]() , so that
, so that
![]() . If
. If
![]() we
have
we
have
![]() and again
and again
![]() , so
, so
![]() .
Thus damping increases
.
Thus damping increases ![]() when
when
![]() (so that the maximum of the response comes after the maximum of the
force) and decreases
it when
(so that the maximum of the response comes after the maximum of the
force) and decreases
it when
![]() (so that the maximum of the response
comes before the minimum of the force). When
(so that the maximum of the response
comes before the minimum of the force). When
![]() we have
we have
![]() and
and
![]() .
.
For any given ![]() and
and ![]() the amplitude of the steady
state solution will be less than the amplitude of the corresponding solution
of the undamped system, and as the damping constant
the amplitude of the steady
state solution will be less than the amplitude of the corresponding solution
of the undamped system, and as the damping constant ![]() increases
the amplitude will decrease (because
increases
the amplitude will decrease (because ![]() is an increasing function
of
is an increasing function
of ![]() ). If you keep
). If you keep ![]() ,
, ![]() and
and ![]() fixed and allow
fixed and allow ![]() (and thus
(and thus ![]() ) to vary, it's easy to see that the maximum amplitude
will occur when
) to vary, it's easy to see that the maximum amplitude
will occur when
![]() .
.
On the other hand, if you fix ![]() ,
, ![]() and
and ![]() and
allow
and
allow ![]() to vary, it's not so easy to see where the maximum
amplitude will occur. To maximize the amplitude we want to minimize
to vary, it's not so easy to see where the maximum
amplitude will occur. To maximize the amplitude we want to minimize
![]() . We may as well minimize
. We may as well minimize
![]() . Letting
. Letting ![]() for convenience, we have
for convenience, we have
![]() so
so
Thus we have seen three effects of damping on forced vibrations: