First Order Linear Differential Equations

There is no general method for solving all differential equations. Instead, just as with integration, there is a collection of techniques, each of which applies to a particular class of equations. We'll look at a couple of these techniques. The first one applies to first order linear equations. The general first order linear equation can be written as y' + p(t) y = q(t) where p(t) and q(t) are arbitrary functions of t.

The solution is as follows: let $\mu(t) = \exp\left(\int p(t)\, dt\right)$This is called an integrating factor. Then the solution is

$$y = \frac{1}{\mu(t)} \left( \int \mu(t) q(t)\, dt + C\right)$$

Here C is the arbitrary constant that goes along with the indefinite integral. You might ask, why isn't there another arbitrary constant with the integral in $\mu(t)$? There could be one, but it wouldn't matter: different choices of that constant would end up giving you the same solutions. But the constant C is important, because different choices of C give different solutions.

Example 1: Solve

$$\frac{dy}{dt} + 2 t y = 4 t$$

Here p(t) = 2 t and q(t) = 4 t. First step: find the integrating factor.

$$\mu(t) = \exp\left(\int 2 t dt\right) = \exp(t^2)$$

Second integration:

$$\int \mu(t) q(t)\, dt = \int 4 t \exp(t^2)\, dt = 2 \exp(t^2) + C$$

So the answer is:

$$y = \exp(-t^2) \left( 2 \exp(t^2) + C \right) = 2 + C \exp(-t^2)$$

If you are given an initial value y(t₀) = y₀ in addition to the differential equation, you have an initial value problem. Then after obtaining the general solution as above, you use the initial value to determine what C is. For example, in the last equation, suppose we had the initial value y(1)=4. Then we would set y=4, t=1 to get $4 = 2 + C \exp(-1)$so $C=2 \rm e$. Thus the solution is

$$y = 2 + 2 \exp(-t^2 + 1)$$

Why it works

For convenience I'm going to leave out all the (t)'s, so just remember that everything is supposed to be a function of t. Suppose we multiply the equation by $\mu$:

$$\mu y' + p \mu y = \mu q$$

Note that $(\mu y)' = \mu y' + \mu' y$.We cleverly defined $\mu$ so that $\mu' = p \mu$. So the left side of the equation becomes $(\mu y)' = \mu q$.Now we can integrate both sides:

$$\mu y = \int \mu q \, dt + C$$

Divide by $\mu$, and you have the solution formula.

Special Cases:

The formula becomes a bit simpler if q(t) = 0: the differential equation is then called a homogeneous linear equation. Of course the antiderivative of is 0 + C (don't forget that C). So the solution is

$$y = C/\mu(t)$$

For example:

$$y' + \sin( t) y = 0$$

We then have

$$\mu(t) = \exp \left( \int \sin t \, dt \right) = \exp(-\cos t)$$

so the solution is

$$y = C \exp(\cos t)$$

Another important special case is when p is a constant. Then we have a constant-coefficient linear equation. The first integration is easy:

$$\mu(t) = \exp(p t)$$

For example, we solve the initial value problem:

$$y' + 3 y = t \qquad y(0) = 1$$

The integrating factor is $\mu(t) = \exp(3 t)$, so we have to integrate

$$\displaylines{\int \mu(t) q(t)\, dt = \int t {\rm e}^{3 t}\,... ...\frac{t}{3} {\rm e}^{3 t} - \frac{1}{9} {\rm e}^{3 t} + C \cr}$$

(how did I get that?)

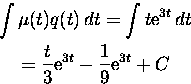
Thus the general solution is

$$\displaylines{ y = {\rm e}^{-3 t} \left( \frac{t}{3} {\rm e}... ...\right)\cr = \frac{t}{3} - \frac{1}{9} + C {\rm e}^{-3 t} \cr}$$

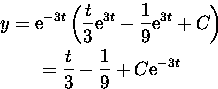
Plugging in the initial conditions: 1 = 0 - 1/9 + C, C = 10/9 so the answer is

$$y = \frac{t}{3} - \frac{1}{9} + \frac{10}{9} {\rm e}^{-3 t}$$