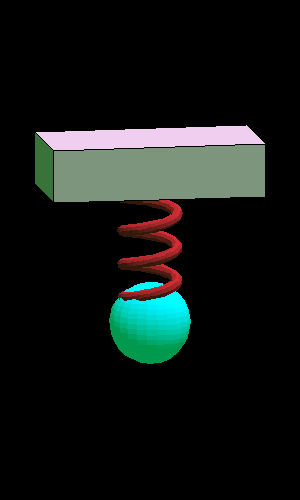

Gravity acts with a force ![]() downwards on the mass. Moving the mass down stretches the spring, and
according to Hooke's Law the spring exerts a force in the opposite
direction, proportional
to the amount of stretching. The spring constant
downwards on the mass. Moving the mass down stretches the spring, and
according to Hooke's Law the spring exerts a force in the opposite
direction, proportional
to the amount of stretching. The spring constant ![]() is the force per unit
of stretching (a positive number).
The mass can hang motionless
at a certain equilibrium position,
at which the forces of gravity and the spring are in balance:
is the force per unit
of stretching (a positive number).
The mass can hang motionless
at a certain equilibrium position,
at which the forces of gravity and the spring are in balance: ![]() , where
, where
![]() is the amount of stretching. We take this equilibrium position as the
origin of our coordinate system: our dependent variable
is the amount of stretching. We take this equilibrium position as the
origin of our coordinate system: our dependent variable ![]() is the displacement
of the mass away from the equilibrium position. Boyce and DiPrima take
a downward
displacement as positive, but I always prefer to take up as positive.
is the displacement
of the mass away from the equilibrium position. Boyce and DiPrima take
a downward
displacement as positive, but I always prefer to take up as positive.
Now if the mass is displaced by ![]() , the spring's force is
, the spring's force is ![]() while gravity is still
while gravity is still ![]() , and the net force is
, and the net force is ![]() . If there are no other
forces acting on the mass, by Newton's second law we get the differential
equation
. If there are no other
forces acting on the mass, by Newton's second law we get the differential
equation
In most real situations, there are other forces acting on the mass that
tend to resist the motion and would cause it to die out eventually. For
example, there probably is some air resistance. Or some damping mechanism
might be deliberately introduced (e.g. the shock absorbers on your car).
Whatever produces this damping force, we assume that it is proportional to the
velocity and in the opposite direction, with a positive constant ![]() measuring
the force per unit of velocity. Then the differential equation becomes
measuring
the force per unit of velocity. Then the differential equation becomes
There may also be an external force that can depend on time but not on
![]() or its derivatives. If this force is
or its derivatives. If this force is ![]() , the equation is
, the equation is
Similar equations govern oscillations in electrical circuits. Consider a voltage source, resistor, inductor and capacitor in series.
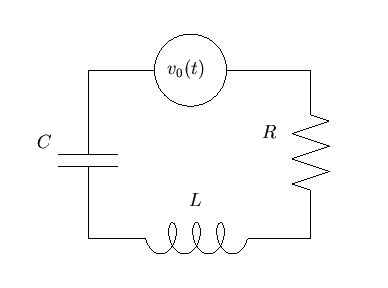
If ![]() is the
current in the circuit, the voltage drop across the resistor is
is the
current in the circuit, the voltage drop across the resistor is ![]() and
that across the inductor is
and
that across the inductor is ![]() , where
, where ![]() is the resistance and
is the resistance and ![]() the inductance. The voltage drop across a capacitor of capacitance
the inductance. The voltage drop across a capacitor of capacitance ![]() is
is
![]() where
where ![]() is the charge on the capacitor. Now
is the charge on the capacitor. Now ![]() (current is
the rate
of flow of charge) so the total voltage drop across resistor, inductor and
capacitor is
(current is
the rate
of flow of charge) so the total voltage drop across resistor, inductor and
capacitor is
![]() . This must be equal to the voltage across
the source, say
. This must be equal to the voltage across
the source, say ![]() . We have the differential equation
. We have the differential equation
Free Undamped Vibrations
Another way to write the
solutions comes from the complex solution
![]() (where
(where ![]() is any complex constant). Write
is any complex constant). Write ![]() in its polar representation as
in its polar representation as
![]() where
where ![]() and
and ![]() is real. Then
is real. Then
![]() . The real part
of
. The real part
of ![]() , which is also a solution,
is
, which is also a solution,
is
![]() .
. ![]() is called the amplitude of the
solution and
is called the amplitude of the
solution and ![]() the phase. Note that
the phase. Note that ![]() varies from
varies from ![]() to
to ![]() ,
with
,
with ![]() when
when
![]() for any integer
for any integer ![]() .
.
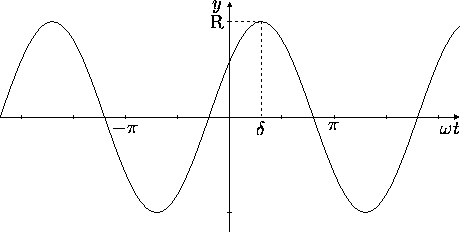
Of course, this is just another way to write the same general solutions.
Using the trigonometric identity for cosine of a difference,
![]() so
so
![]() and
and
![]() .
.
Free Damped Vibrations
 . If we call the roots
. If we call the roots Click on the picture for an animation.
 .
Thus
.
Thus
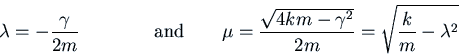
The picture below shows a solution with ![]() ,
, ![]() ,
, ![]() ,
resulting in
,
resulting in ![]() and
and ![]() . The quasi-period is
. The quasi-period is
![]() .
.
Click on the picture for an animation.