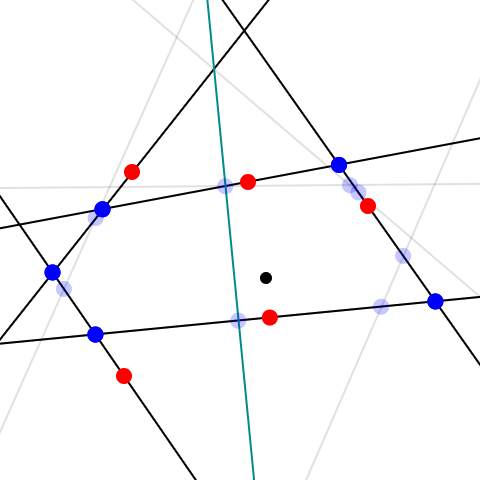

The 'axiality' of a bounded convex set in ℝ² is the maximal overlap the body may have with itself when reflected about a line. For example, many shapes you might think of (regular polygons, ellipses, isosceles triangles) are completely axial, as there is a line relfecting them on top of themselves. For others, such as scalene triangles and parallelograms, there is no way to do this. A question is, among all convex sets, how small may the largest possible overlap be? It is an interesting problem to search for shapes with the least amount of symmetry possible. It was shown in our paper that no matter what the shape is, there is always a line that results in at least 69% overlap.
On the other hand, it was shown that for some special triangles and paralleorams, there may be no line that gives more than 82.8% overlap, and for many years this was thought to be optimal. It was even shown to be the lowest possible axiality for centrally symmetric bodies. However, in his masters thesis, Choi improved this upper bound to approximately 0.81584 using a computer program. He made a new conjecture, that the true value of the minimal axiality in the plane "c(2, 1)" is around 0.81. Our paper has a construction of an exact family of shapes with axiality as low as 0.8047, but along the way we found extremely low symmetry shapes computationally.
The search that Choi implemented to find low symmetry shapes was not explained in his thesis, but we speculate that the computational intensity of obtaining the axiality of a given shape may have prevented him from finding something better. We found a simple technique to estimate the axiality much faster than normal (which is controlled by 'iters3' in the program, see usage below), and using this we were able to impliment a basic algorithm using simulated annealing to iteratively search for low symmetry shapes. This proved extremely effective, quickly finding shapes of symmetry around 0.808. Going lower took increasingly more patience, but we eventually found shapes under 0.806, one of which is loaded when the program opens.
The process of bounding the axial symmetry, in short, can be done by checking a suitably fine sample of potential lines to reflect the shape in. Once a rotation for the line has been chosen, finding the optimal translation of it becomes a matter of finding the maximum of a unimodal function, which can be done very quickly and precisely. So the main source of computational intensity comes from using enough angles so that there is very little gap between the directions tested.
One can use this program to compute the axial symmetry of a shape accurate within an error of ε = 10-5. The process of verifying the value has three sources of error, the first of which is massively subsumed by the following two if we are asking for only five decimal places of accuracy. They are
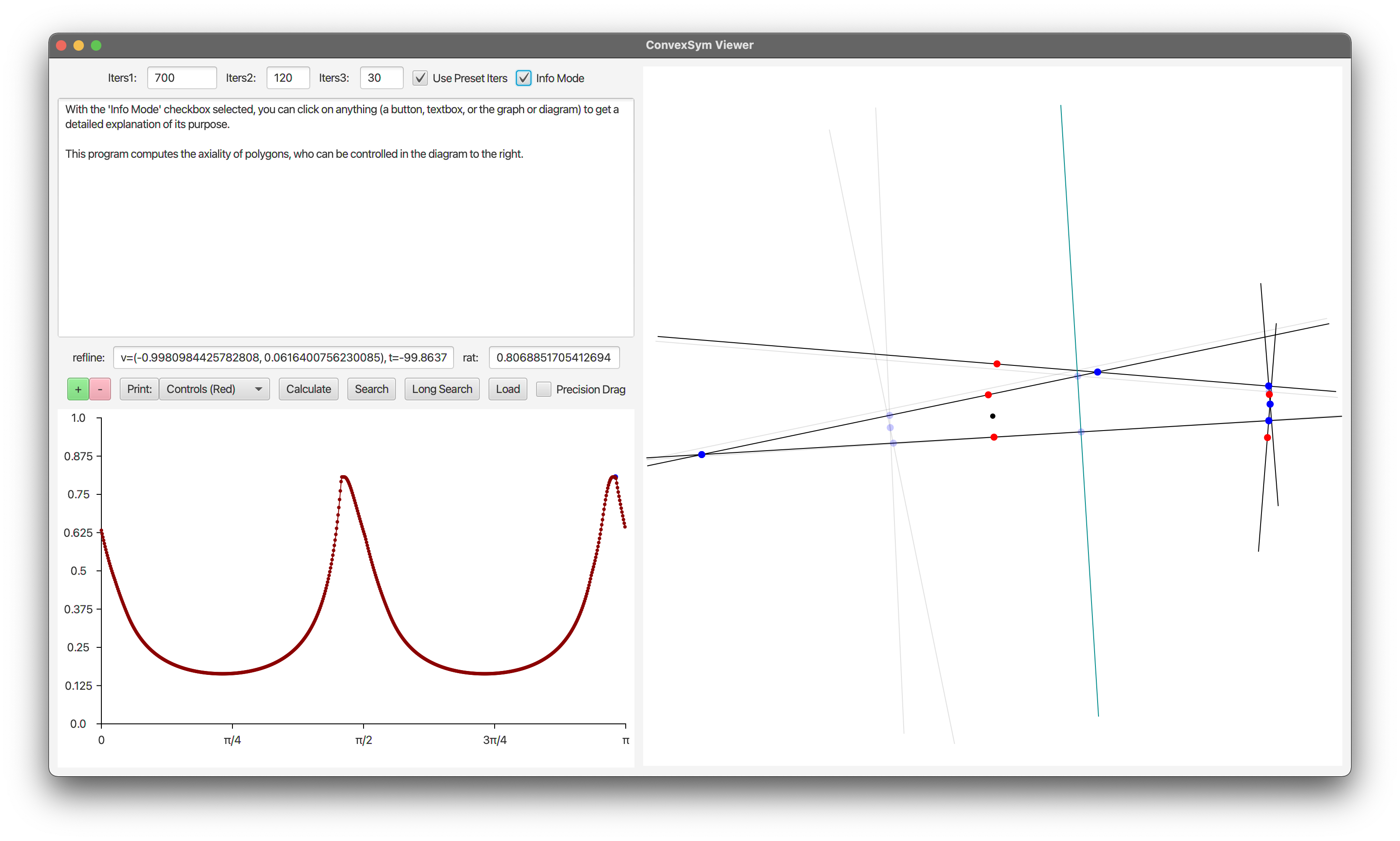
This program was intended to be distributed alongside our paper, and as such it is very user friendly. Every control in the program has a detailed explanation that can be accessed while using it; by having the Info Mode checkbox selected, you can click on anything to see a detailed explanation.
One can use this program to easily modify the convex quadrilateral loaded when the progmram opens and run our searching algorithm from initial conditions with any number of sides. There is a chance one could find another shape with less axial symmetry than the final construction in our paper, even while just using our program. However, our search has been sufficiently exhaustive that we believe a shape with symmetry much lower than ours is unlikely. If one desires to verify the axiality of a shape, one should run the exact test of it. To do so, the following quantities should be set: