


Next: Properties of the solution
Up: If counting polyominoes is
Previous: If counting polyominoes is
Many problems are too difficult to be tackled analytically, and often the most appropriate
avenue to take is some sort of numerical analysis or random simulation. Even if we are
unable to solve a model, it is frequently possible to write a reasonably fast computer
algorithm to provide us with the first 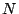 coefficients of the generating function,
coefficients of the generating function,
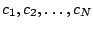 , either exactly11 or to a good approximation12.
, either exactly11 or to a good approximation12.
It is sometimes possible, from the first 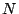 terms (if they are exact), to somehow ``see''
the pattern in the coefficients and hypothesise a solution (which can then be proved by
other means). More usual is to use the data to explore the asymptotic behaviour of the
model. One can make some assumption about the asymptotic form of the coefficients such as
terms (if they are exact), to somehow ``see''
the pattern in the coefficients and hypothesise a solution (which can then be proved by
other means). More usual is to use the data to explore the asymptotic behaviour of the
model. One can make some assumption about the asymptotic form of the coefficients such as
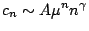
as
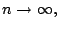
and then fit the data (exact or approximate) to this form and so obtain estimates of
various quantities such as the growth constant or the mean geometric
size13 of the objects. Indeed for many purposes the asymptotic behaviour of a model
is arguably more interesting than the existence of an exact solution (particularly if we
are modelling some sort of physical problem). Of course, an exact solution is more useful
than a knowledge of the asymptotic behaviour, since one can (usually) extract the asymptotic
behaviour from a solution but not vice-versa14.



Next: Properties of the solution
Up: If counting polyominoes is
Previous: If counting polyominoes is
Andrew Rechnitzer
2002-12-16
![]() terms (if they are exact), to somehow ``see''
the pattern in the coefficients and hypothesise a solution (which can then be proved by
other means). More usual is to use the data to explore the asymptotic behaviour of the
model. One can make some assumption about the asymptotic form of the coefficients such as
terms (if they are exact), to somehow ``see''
the pattern in the coefficients and hypothesise a solution (which can then be proved by
other means). More usual is to use the data to explore the asymptotic behaviour of the
model. One can make some assumption about the asymptotic form of the coefficients such as