- ... grid1
- Due to limitations of space, we cannot show all
of it here.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
heuristic2
- i.e. hand-waving.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...machinery3
- It could be a mathematical, virtual, quantum...it really
doesn't matter.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... way4
- Other than giving up.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... list5
- Any method that is ``slower'' than this really is
worthless.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... evaluate''6
- Since
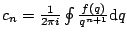 ,
we can recover
,
we can recover 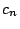 from the expression of
from the expression of 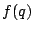 or
or 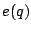 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... bounds7
- This topic is evolving rapidly; see Steve Finch's web page on mathematical
constants for up-to-date information ( http://www.mathsoft.com/asolve/constant/constant.html )
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...space8
- i.e. the amount of computer memory required to compute
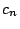 also grows exponentially with
also grows exponentially with 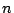 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
Ideally9
- In a perfect world where our brains are larger...well even this may
not be enough; no-one has proved that a good solution exists.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... frustrated10
- This is an understatement of the extreme difficulty that
has been encountered by those venturing into this area of enumerative combinatorics.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... exactly11
- In which case
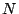 is probably a small integer,
probably well under
is probably a small integer,
probably well under 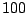 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... approximation12
- In which case
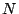 is
probably much larger, but the error bounds on the estimates of the coefficients also
become larger and larger with
is
probably much larger, but the error bounds on the estimates of the coefficients also
become larger and larger with 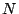 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
size13
- i.e. on average how wide are they? And how does this width change
with
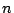 ?
?
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...vice-versa14
- Extracting asymptotic
behaviour from a solution is not necessarily trivial -- indeed for the problems
described in chapter 6, we expect the asymptotics to be rather simple,
but the form of the solution makes proving this rather difficult.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... lattice15
- The square grid is dual to itself, while the dual of
triangular grid is the hexagonal grid (and vice versa).
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... two16
- Spiral walks on the
square and triangular lattices [22,27,42,5,28]
and
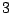 -choice polygons on the square lattice [8].
-choice polygons on the square lattice [8].
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... polyominoes17
- One can also solve directed polyominoes whose
cells lie on or below the line
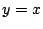 ; these arise in the solution of directed
polyominoes.
; these arise in the solution of directed
polyominoes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... lattices18
- Using lattice duality square and hexagonally celled
directed polyominoes are also solved.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... below19
- A cell is supported only from below if
there is another cell directly below it, but no cell directly on its left.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... polyominoes20
- Column-convex polyominoes are always
polygons.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... interesting21
- On the
square lattice there are
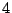 directions that each bond may take, and then
directions that each bond may take, and then 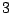 possible directions for the following bond (since immediate reversal of direction
would violate self-avoidance), and so there are
possible directions for the following bond (since immediate reversal of direction
would violate self-avoidance), and so there are 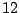 possible two-step
configurations. The different TSRW models are obtained by allowing or
disallowing each of these
possible two-step
configurations. The different TSRW models are obtained by allowing or
disallowing each of these 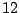 configurations. Hence there are
configurations. Hence there are
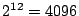 different TSRW models on the square lattice! Most of these are essentially either
zero- or one-dimensional.
different TSRW models on the square lattice! Most of these are essentially either
zero- or one-dimensional.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... model22
- Since there are both
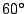 and
and 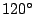 turns on the triangular lattice,
there are three possible models of spiral walks (depending on which of these turns is
allowed). -- the solved model allows only
turns on the triangular lattice,
there are three possible models of spiral walks (depending on which of these turns is
allowed). -- the solved model allows only 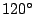 turns.
turns.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
polygons23
- Polygons that are both row-convex and column-convex are called
convex polygons -- this is an ambiguous convention.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... functions24
- In the case of polygon models and bond-animals, this generating
function enumerates animals according to the number of vertical and horizontal bonds.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... transparent25
- In the sense of being a very direct application of
animals and polyominoes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... size26
- Not the number of monomers, rather a measure of the space occupied
by the polymer.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... gyration27
- Other measures of
the size of a polymer are expected to behave similarly.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... any28
- Any linear
polymer that is flexible and has short-range interactions.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... solved29
- It has not been
entirely solved; some properties of the model have been found -- the free energy and
spontaneous magnetisation -- while others -- most notably the susceptibility -- remain
unknown.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...30
- Since we consider only a finite portion of the lattice, the number of nearest-neighbour
pairs is finite, and so the sum is convergent.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.