Placing tiles

Consider an infinite square grid¹, and some unit square tiles.

Figure 1: A portion of the infinite square grid, and some square tiles.

This thesis (and a good number of other theses and articles) is motivated by the simple question:

Question 1   How many ways can we place a finite number of tiles on the square grid?

Rather than leaping in at the deep end, let us start with a simpler question:

Question 2   How many ways can we place a single tile on the square grid?

Figure 2: A placement of a single tile on the square grid.

Since there are an infinite number of cells on the square grid, and a single tile can be placed on any of them, there are an infinite number of ways we can place a single tile. All of these different ways, however, are equivalent under translation -- there is only a single way to colour a single cell (up to translation).

Figure 3: These two arrangements of five tiles are equivalent up to translation.

In the same way, both of the arrangements in figure 3 are equivalent under some translation. In light of this, let us modify question 1:

Question 3   How many ways (up to translation) can we place a finite number of tiles on the square grid?

We know that there is only a single way to place a single tile (up to translation). What about placing two tiles? Consider the three arrangements in figure 4. The tiles in the first two arrangements (left and centre) touch, while in the last the tiles are separated by at least a single lattice spacing. It is not difficult to see that there are only two connected arrangements of two tiles. Let us define connectedness a little more carefully:

Figure 4: The first two arrangements are the only possible connected arrangements of two tiles. Disconnected arrangements pose problems -- there are an infinite number of disconnected arrangements of two tiles.

Definition 1
We say that an arrangement of tiles, $P$, on the square grid is connected if for any two tiles in $P$ there exists a path (made up of unit steps north, east, south or west) from one tile to the other, that stays completely within $P$ (see figure 5).

If an arrangement of $n$ tiles is connected, then we call it an $n$-celled polyomino, or a polyomino of area $n$. Unless explicitly stated otherwise, we will consider polyominoes defined up to translation (i.e. if polyomino $\char93 1$ can be mapped to polyomino $\char93 2$ under some translation, then we will consider them to be the same).

The name, polyomino, was introduced by Golomb [14], and is the generalisation of dominoes.

Figure 5: The arrangement on the left is connected, while that on the right is not.

Lemma 1   For finite $n$, there is always a finite number of polyominoes of area $n$. More specifically, there cannot be more than $\binom{n^2}{n}$ polyominoes of area $n$.

A polyomino of area $n$ must always be contained within a square ``box'' of side-length $n$; this box contains $n^2$ cells. Every polyomino is a choice of $n$ cells from within this box and so there are at most $\binom{n^2}{n}$ polyominoes of area $n$. $\hfill{\vrule height 3pt width 5pt depth 2pt}$

Figure 6: The $6$ possible polyominoes of area $3$.

On the other hand, we can easily create an infinite number of disconnected arrangements of two tiles -- take the single arrangement of a single tile, and then place another tile $n$ cells to its right, where $n$ is some integer strictly greater than $1$. Using similar reasoning, it is not hard to see that there will always be an infinite number of disconnected arrangements of $n$ tiles (for finite $n \geq 2$) .

Since there are always a finite number (up to translation) of polyominoes of area $n$, and an infinite number of disconnected arrangements of $n$ tiles, we modify question 3:

Question 4   How many different polyominoes (up to translation) of area $n$ can be constructed on the square grid?

Before we consider what is known about the number of polyominoes, let us first consider what we would accept as a solution to question 4.

Question 5   What constitutes a solution to question 4?

Rather than delving into a deep discussion of computational complexity and mathematical philosophy, we will attempt to answer this question in a heuristic² way.

Any answer to question 4 must be a two step process of the form:

$\mathbf{1 \rightarrowtriangle}$

choose some $n \in \mathbb{N}$.

$\mathbf{2 \rightarrowtriangle}$

put this $n$ into some sort of machinery³ and after some finite amount of time it returns the number, $c_n$, of polyominoes of area $n$.

This ``definition'' of a solution clearly allows a very wide range of possibilities -- ideally we would like to find the ``best'' possible solution, however this is really hard to define. It is much easier to start with the ``worst'' type of solution. Perhaps the ``worst'' way⁴ in which we can compute $c_n$ is to use brute force to list all of the polyominoes with $n$ cells; $c_n$ is then the length of the list⁵. For many problems no better method is forthcoming and this ``worst'' method is in fact the best available.

Any method that is ``faster'' than this ``worst'' approach (particularly when $n$ is a large number) is, in some weak way, a solution; combinatorialists consider a nice solution to be one of the following:

• a closed-form expression for $c_n$ that is ``easy to evaluate'',
• a closed-form expression for the generating function,
  $$f(q) = \sum c_n q^n$$   or$$\qquad \qquad e(q) = \sum c_n \frac{q^n}{n!}$$
  that is ``easy to evaluate''⁶, or
• an algorithm or recurrence that computes $c_n$ ``efficiently'' (and may be equivalent to a closed-form expression for $c_n$ or the generating function).

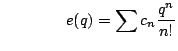
By an expression being ``easy to evaluate'' we mean that evaluating the expression should be substantially faster than the brute force method -- if we wish to compute all the elements in a set $S$, then a solution of the form

$$\vert S\vert = \sum_{x \in S} 1,$$

is equivalent to brute force and so is almost completely worthless.

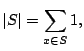
Another slightly different way of ``solving'' a polyomino problem (which we do not explore in this thesis) is to somehow map the original problem to a new problem that can be solved. A solution to the new problem may not give us a means of calculating $c_n$, but it may give us exact values of other quantities of interest, such as growth constants and critical exponents (see section 2.2 below).

As an example of the different forms of a solution, let us consider the simpler question of permutations:

Question 6   What is the number, $\mathbf{s_n}$, of ways of ordering $\mathbf{n}$ objects?

The ``worst'' solution to this problem of computing $s_n$ would be to list all the possible permutations using a computer program (or, heaven forbid, by hand). A better solution would be to show that the numbers $s_n$ satisfy the recurrence

$$s_0 = 1,$$

$$s_n = n s_{n-1} \mbox{for $n \geq 1$} .$$ (1)

Solving this recurrence gives a closed-form expression for $s_n$ that is very easy to evaluate:

$$s_n = n!$$ (2)

Alternatively we could solve the recurrence for the (exponential) generating function,

$$\sum_{n\geq0} s_n \frac{q^n}{n!} = \sum_{n\geq0} q^n = \frac{1}{1-q}.$$ (3)

Any solution to question 4 that took one of these three ``compact'' and ``efficient'' forms (i.e. a closed form expression for the coefficients or the generating function, or an efficient algorithm) would be most welcome. In this thesis we will almost exclusively consider solutions in terms of generating functions.

Question 7   What do we know about the number of polyominoes?

In one dimension, it is easy to see that there is only a single $n$-celled polyomino for any given $n$. As soon as one ventures into two or more dimensions, however, the answer is not so simple; it may come as a surprise that the answer to question 4 remains elusive even after more than $40$ years of intensive study [15,29,40]. Arguably the strongest rigorous result on the number of polyominoes concerns their asymptotics. Let $c_n$ denote the number of polyominoes of area $n$ on the square lattice. A concatenation argument [30] shows that

$$c_{n+m} \geq c_n \; c_m \qquad \qquad \forall n,m \in \mathbb{N}.$$

Combining this with a better upper bound than that given in lemma 1 implies that there exists a constant $\mu$, sometimes called Klarner's constant, or more generally growth constant and connective constant, such that

$$\lim_{n \rightarrow \infty} (c_n)^{1/n} = \mu.$$

The exact value of $\mu$ is unknown, though numerical studies [9,26] have shown that $\mu \simeq 4.06$. The best published bounds⁷ for $\mu$ [26,31] are

$$3.9 < \mu < 4.65.$$

It is a measure of the complexity of polyomino enumeration that after more than forty years, the rigorous bounds on $\mu$ are so wide (we only know it to within around $20\%$ of the value predicted by numerical work).

The existence of $\mu$ tells us that the number, $c_n$, of polyominoes of area $n$ grows exponentially with $n$; for any $\bar{\mu} < \mu$ we have (for sufficiently large $n$) $c_n > \bar{\mu}^n$. There are lots of them! It also allows us be a little more specific about what we would require of a good solution to question 4.

Since the number of polyominoes grows exponentially, the time taken by a brute-force approach must also grow exponentially (time $= O(\mu^n)$). Consequently, any method that evaluates $c_n$ in either bounded time (time $= O(1)$) or polynomial time (time $= O(n^\alpha)$, for some $\alpha \in \mathbb{R}^+$) would be a very good answer to question 4. Even an exponential time algorithm (time $= O(\lambda^n)$, for some $1 < \lambda < \mu$) would be, in some weak sense, a solution. The best ``solution'' to date (in two dimensions) is an enumeration algorithm based on the finite lattice method [9] -- this still requires exponential time and space⁸, but is exponentially faster than brute force enumeration.

Since the enumeration of polyominoes (and related objects) in one dimension is trivial, in this thesis we mostly consider enumeration problems in two dimensions (on the square, triangular and honeycomb lattices).