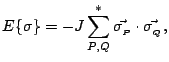Next: Bibliography
Up: Why do we want
Previous: Polymer models
The last example we will consider is the Ising model. Unlike the previous three examples
in which animal and polyomino enumeration arise quite directly, one must venture a little
way beyond the definition of the Ising model before the animals can be found lurking.
The Ising model is perhaps the most famous and widely studied model in statistical mechanics. It
models the effect of temperature and external magnetic fields on the properties of a
magnet. When a piece of iron is placed in a magnetic field it becomes magnetised. If the
magnet is then heated, the strength of the iron's magnetic field weakens until it
disappears -- the temperature at which this happens is called the Curie temperature. This
change in behaviour is much like the transition water undergoes when it evaporates, and
is known as a phase transition. Phase transitions are also observed in
combinatorial models and exhibit themselves as changes in their asymptotic behaviour.
The Ising model was solved in one dimension by Ising [24], but was shown not to
undergo any phase transition. Onsager [34] solved29 the two dimensional Ising model (in the case of no external magnetic field),
and it was shown to undergo a phase transition like those exhibited by real magnets. The
three dimensional Ising model remains unsolved.
Let us demonstrate how animals arise in this model. Consider a finite portion of the
square lattice with magnetic ``spins'' placed at the vertices. These spins could be
vectors, scalars or even quantum mechanical spin operators. The Ising model considers
only the simplest case; each spin is either spin up (
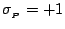 ) or spin down
(
) or spin down
(
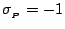 ) (see figure 22).
) (see figure 22).
The interaction energy of a configuration
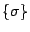 is defined to be
is defined to be
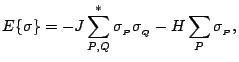 |
(10) |
where
 denotes the sum over all pairs of nearest neighbour spins,
denotes the sum over all pairs of nearest neighbour spins,  and
and  30,
30, 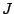 is the ``coupling constant'' that defines the strength of the interaction
between spins, and
is the ``coupling constant'' that defines the strength of the interaction
between spins, and 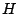 represents the interaction between the spins and the external
magnetic field (if there is one).
represents the interaction between the spins and the external
magnetic field (if there is one).
The key to any statistical mechanical problem is the computation of the partition
function which is given by
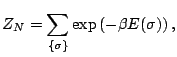 |
(11) |
where the sum is over all possible configurations, 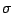 , of the system,
, of the system,
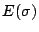 is the energy of a given configuration,
is the energy of a given configuration, 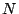 is the number of sites in the
lattice,
is the number of sites in the
lattice,
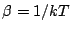 ,
, 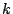 is Boltzmann's constant and
is Boltzmann's constant and 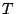 is the absolute
temperature. A knowledge of the partition function of a system is sufficient to find
many other relevant thermodynamic quantities, such as the internal energy and
entropy.
is the absolute
temperature. A knowledge of the partition function of a system is sufficient to find
many other relevant thermodynamic quantities, such as the internal energy and
entropy.
Onsager's solution of the two dimensional Ising model in zero external field (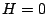 ) is
far from trivial, and we will not discuss it in this thesis (except for a brief discussion
of transfer matrices in chapter 8). Van der Waerden [41] showed
how the evaluation of the partition function can be translated into a bond animal
enumeration problem. We give an outline of this approach.
) is
far from trivial, and we will not discuss it in this thesis (except for a brief discussion
of transfer matrices in chapter 8). Van der Waerden [41] showed
how the evaluation of the partition function can be translated into a bond animal
enumeration problem. We give an outline of this approach.
When 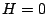 the partition function becomes
the partition function becomes
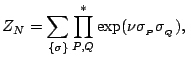 |
(12) |
where
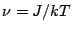 and
and
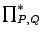 denotes the product over all pairs of
nearest-neighbour spins,
denotes the product over all pairs of
nearest-neighbour spins,  and
and  . It is not difficult to verify that
. It is not difficult to verify that
Using this we can rewrite the partition function as
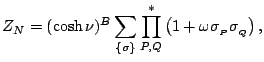 |
(14) |
where
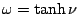 , and
, and 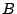 is the number of bonds in the lattice. From here
it is not hard to rewrite this as a sum over graphs on the square grid.
is the number of bonds in the lattice. From here
it is not hard to rewrite this as a sum over graphs on the square grid.
Figure 23:
Typical graphs that contribute to the partition function -- some of these
graphs are self-avoiding polygons. It is possible for the graphs to be
disconnected.
|
|
Let us consider each bond on the grid to be either occupied or vacant, and let 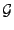 be
the set of all possible combinations of occupied bonds (each combination forms a graph
with vertex set equal to the
be
the set of all possible combinations of occupied bonds (each combination forms a graph
with vertex set equal to the 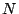 sites in the lattice). Note that though these graphs are
similar to bond animals, they are not bond animals, since they can be disconnected and
they are not translationally invariant. The partition function can be rewritten as
sites in the lattice). Note that though these graphs are
similar to bond animals, they are not bond animals, since they can be disconnected and
they are not translationally invariant. The partition function can be rewritten as
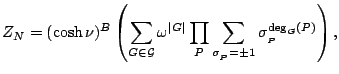 |
(15) |
where 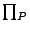 is a product over all
is a product over all 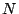 sites,
sites, 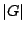 is the number of occupied bonds in
is the number of occupied bonds in
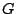 and
and 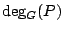 is the number of occupied bonds incident on the vertex
is the number of occupied bonds incident on the vertex 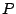 in the
graph
in the
graph 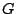 . Now, for any spin
. Now, for any spin
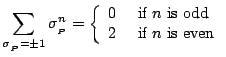 |
(16) |
and so when we sum over the possible spin configurations in equation (15),
any graph, 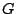 , that has a vertex of odd degree will contribute zero while all
other graphs will contribute
, that has a vertex of odd degree will contribute zero while all
other graphs will contribute 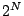 . Let us define
. Let us define
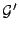 to be the subset of
to be the subset of 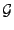 such
that for every
such
that for every
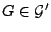 every vertex in
every vertex in 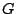 has even degree. If we define
has even degree. If we define 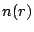 to be
the number of graphs in
to be
the number of graphs in
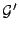 that contain
that contain 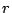 bonds, then the partition function is
bonds, then the partition function is
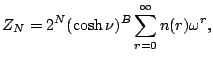 |
(17) |
where 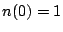 . So the problem has been reduced to finding the generating function of a
set of graphs, which are related to bond animals (though they are not restricted to be
connected, nor are they defined up to translation). These graphs (see figure
. So the problem has been reduced to finding the generating function of a
set of graphs, which are related to bond animals (though they are not restricted to be
connected, nor are they defined up to translation). These graphs (see figure ![[*]](file:/usr/local/share/lib/latex2html/icons/crossref.png) ) look like self-avoiding polygons, or groups of overlapping self-avoiding
polygons -- in fact, self-avoiding polygons were introduced by Temperley [40] as
a special case of these graphs.
) look like self-avoiding polygons, or groups of overlapping self-avoiding
polygons -- in fact, self-avoiding polygons were introduced by Temperley [40] as
a special case of these graphs.
Figure 24:
Typical graphs that contribute to the correlation function -- some may be
self-avoiding walks. The vertices of odd degree are highlighted.
|
|
Another quantity of interest is the pair correlation function,
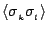 , which is defined by
, which is defined by
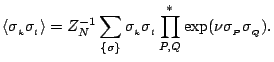 |
(18) |
This function is a measure of the degree of order within the state of the system --
if there is long range order in the system, then separated spins will tend to be in
the same state and the pair correlation function will take a value bounded away from
0. Following the same argument used for the partition function, we can rephrase the
pair correlation function as the generating function of a new set of graphs in which
every vertex is of even degree excepting 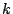 and
and 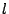 , which must be of odd
degree (see figure 24). In the same way that self-avoiding polygons
arose in the partition function, we find that self-avoiding walks arise in the graphs
contributing to the pair correlation function.
, which must be of odd
degree (see figure 24). In the same way that self-avoiding polygons
arose in the partition function, we find that self-avoiding walks arise in the graphs
contributing to the pair correlation function.
The 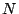 -vector model discussed above is a generalisation of the Ising model, in which the
spins can take one of
-vector model discussed above is a generalisation of the Ising model, in which the
spins can take one of 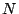 states. These
states. These 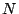 states are equally spaced unit vectors in
states are equally spaced unit vectors in
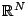 , and the interaction energy of a configuration
, and the interaction energy of a configuration
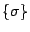 is defined to
be
is defined to
be
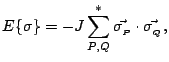 |
(19) |
and so when  we arrive back at the Ising model. In the limit
we arrive back at the Ising model. In the limit
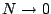 the
the
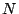 -vector model is equivalent (in some sense) to self-avoiding walks [11].
-vector model is equivalent (in some sense) to self-avoiding walks [11].



Next: Bibliography
Up: Why do we want
Previous: Polymer models
Andrew Rechnitzer
2002-12-16
![]() ) or spin down
(
) or spin down
(
![]() ) (see figure 22).
) (see figure 22).
![]() is defined to be
is defined to be
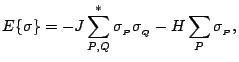
![]() ) is
far from trivial, and we will not discuss it in this thesis (except for a brief discussion
of transfer matrices in chapter 8). Van der Waerden [41] showed
how the evaluation of the partition function can be translated into a bond animal
enumeration problem. We give an outline of this approach.
) is
far from trivial, and we will not discuss it in this thesis (except for a brief discussion
of transfer matrices in chapter 8). Van der Waerden [41] showed
how the evaluation of the partition function can be translated into a bond animal
enumeration problem. We give an outline of this approach.
![]() the partition function becomes
the partition function becomes
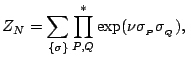
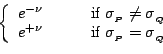
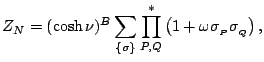
![% latex2html id marker 4035
\includegraphics[scale=0.4]{figs/ising2.eps}](img164.png)
![]() be
the set of all possible combinations of occupied bonds (each combination forms a graph
with vertex set equal to the
be
the set of all possible combinations of occupied bonds (each combination forms a graph
with vertex set equal to the ![]() sites in the lattice). Note that though these graphs are
similar to bond animals, they are not bond animals, since they can be disconnected and
they are not translationally invariant. The partition function can be rewritten as
sites in the lattice). Note that though these graphs are
similar to bond animals, they are not bond animals, since they can be disconnected and
they are not translationally invariant. The partition function can be rewritten as
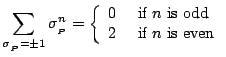
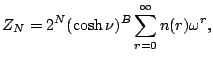
![% latex2html id marker 4083
\includegraphics[scale=0.4]{figs/ising3.eps}](img179.png)
![]() , which is defined by
, which is defined by
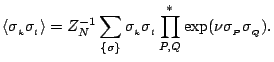
![]() -vector model discussed above is a generalisation of the Ising model, in which the
spins can take one of
-vector model discussed above is a generalisation of the Ising model, in which the
spins can take one of ![]() states. These
states. These ![]() states are equally spaced unit vectors in
states are equally spaced unit vectors in
![]() , and the interaction energy of a configuration
, and the interaction energy of a configuration
![]() is defined to
be
is defined to
be