


Next: Polygons
Up: A taxonomy of the
Previous: Site animals and polyominoes
Figure 13:
The bond animal kingdom -- the only solved models (other than polygon models) are
spiral walks (on the square lattice, and one of the three possible models on the
triangular lattice), partially directed walks and directed walks.
|
|
Like polyominoes and site-animals, bond animals remain unsolved in two dimensions and
higher, it therefore makes sense to consider bond animals with simpler topologies (see
figure 13):
Definition 6
- Directed bond animals are bond animals in which all bonds can be reached
from the vertex at the origin by a path (remaining inside the animal) that takes
only north and east steps.
- Lattice trees are bond animals that contain no closed loops.
- Self-avoiding walks (SAWs) are bond animals with a linear
topology. Alternatively they are bond animals, such that every vertex visited by the
animal is of degree
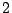 , excepting two vertices (the endpoints) which are of degree
, excepting two vertices (the endpoints) which are of degree
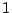 .
.
Unfortunately these restrictions have not been sufficient to lead to a solution
in any dimension higher than one. It is curious that directed bond animals are yet to be solved when
directed site animals have been solved for almost two decades; we discuss possible reasons
for this in chapter 3.
Self-avoiding walks (SAWs) are of considerable importance as a model of linear polymers
(see below) and have been intensively studied for many years. Even though no exact
solution has been forthcoming, a great deal is known about them, by both rigorous and
numerical methods (see [32] and references within) -- for example, the
connection between SAWs and the 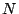 -vector model [11] gives (non-rigorously)
both the critical exponents
-vector model [11] gives (non-rigorously)
both the critical exponents 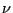 and
and 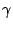 in two dimensions, and the growth constant
on the honeycomb lattice [33].
in two dimensions, and the growth constant
on the honeycomb lattice [33].
Many modified walk models have been introduced to mimic various physical situations
and to allow for easier analysis. These modifications can lead to changes in the
asymptotic behaviour of the model. A large family of modified SAW models are
two-step-restricted walks (TSRWs). A TSRW is constructed by starting at the
origin and adding bonds so that the walk is self-avoiding and so that the possible
directions of the 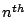 bond (or step) depend upon the direction of the
bond (or step) depend upon the direction of the
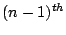 bond according to some rule (consequently the bonds of a TSRW are
ordered). In two dimensions, a wide ranging study of TSRW [21] found
(using computer enumeration and numerical methods) that the asymptotic behaviour of
these TSRWs can be linked to the symmetries of the restricting rule. We describe this
survey in chapter 9. Some of the more interesting21 restricted walks are:
bond according to some rule (consequently the bonds of a TSRW are
ordered). In two dimensions, a wide ranging study of TSRW [21] found
(using computer enumeration and numerical methods) that the asymptotic behaviour of
these TSRWs can be linked to the symmetries of the restricting rule. We describe this
survey in chapter 9. Some of the more interesting21 restricted walks are:
Definition 7
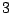 -choice walks are TSRW for which clockwise turns are
forbidden after steps in the
-choice walks are TSRW for which clockwise turns are
forbidden after steps in the 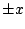 direction; i.e. after an east step it is
not possible to step south, and after a west step it is not possible to step north.
direction; i.e. after an east step it is
not possible to step south, and after a west step it is not possible to step north.
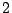 -choice walks are
-choice walks are 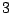 -choice walks that are forbidden to make
more than one successive step in the
-choice walks that are forbidden to make
more than one successive step in the 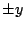 direction.
direction.
- Spiral walks are oriented SAWs in which all clockwise turns are
forbidden; i.e. after an east step it is not possible to step south, after a
north step it is not possible to step east, etc.
- Partially directed walks are SAWs whose intersection with any
vertical line is connected. Equivalently the walk is forbidden to step west.
- Directed walks are SAWs that consist entirely of north and east steps.
These walks are discussed in more detail in chapter 9. The only
``non-trivial'' walk models to have been solved are partially directed walks, directed
walks [37] and spiral walks. Two different spiral walk models have been
solved; spiral walks on the square lattice [22,27,42,5],
and one model22 of spiral walks on the triangular lattice [28] (although the asymptotics of the
other two is known [39]). The growth constants of 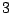 -choice and
-choice and 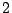 -choice
walks are known [43].
-choice
walks are known [43].
In chapter 9 we examine the behaviour of three dimensional TSRW. There are
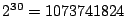 TSRW models in three dimensions, and so we have taken only a
very small subset of these, chosen so as to examine the relationship between
asymptotic behaviour of the walk and the symmetries of the restricting rule. Given the extreme
difficulty of finding rigorous results for any bond animal models, we have used computer
enumeration and numerical methods in this study.
TSRW models in three dimensions, and so we have taken only a
very small subset of these, chosen so as to examine the relationship between
asymptotic behaviour of the walk and the symmetries of the restricting rule. Given the extreme
difficulty of finding rigorous results for any bond animal models, we have used computer
enumeration and numerical methods in this study.



Next: Polygons
Up: A taxonomy of the
Previous: Site animals and polyominoes
Andrew Rechnitzer
2002-12-16
![% latex2html id marker 3596
\includegraphics[scale=0.35]{figs/bond_king.eps}](img90.png)
![% latex2html id marker 3596
\includegraphics[scale=0.35]{figs/bond_king.eps}](img90.png)
![]() -vector model [11] gives (non-rigorously)
both the critical exponents
-vector model [11] gives (non-rigorously)
both the critical exponents ![]() and
and ![]() in two dimensions, and the growth constant
on the honeycomb lattice [33].
in two dimensions, and the growth constant
on the honeycomb lattice [33].
![]() bond (or step) depend upon the direction of the
bond (or step) depend upon the direction of the
![]() bond according to some rule (consequently the bonds of a TSRW are
ordered). In two dimensions, a wide ranging study of TSRW [21] found
(using computer enumeration and numerical methods) that the asymptotic behaviour of
these TSRWs can be linked to the symmetries of the restricting rule. We describe this
survey in chapter 9. Some of the more interesting21 restricted walks are:
bond according to some rule (consequently the bonds of a TSRW are
ordered). In two dimensions, a wide ranging study of TSRW [21] found
(using computer enumeration and numerical methods) that the asymptotic behaviour of
these TSRWs can be linked to the symmetries of the restricting rule. We describe this
survey in chapter 9. Some of the more interesting21 restricted walks are:
![]() TSRW models in three dimensions, and so we have taken only a
very small subset of these, chosen so as to examine the relationship between
asymptotic behaviour of the walk and the symmetries of the restricting rule. Given the extreme
difficulty of finding rigorous results for any bond animal models, we have used computer
enumeration and numerical methods in this study.
TSRW models in three dimensions, and so we have taken only a
very small subset of these, chosen so as to examine the relationship between
asymptotic behaviour of the walk and the symmetries of the restricting rule. Given the extreme
difficulty of finding rigorous results for any bond animal models, we have used computer
enumeration and numerical methods in this study.