A taxonomy of the animal kingdom

Figure 8: Basic bits of grids

Figure 9: Little pictures on grids give rise to polyominoes, site animals and bond animals. Site animals and polyominoes are equivalent under a duality transformation.

Consider again the square grid (see figure 8). On this grid there are three basic graph-theoretic objects -- faces, vertices, edges. In the polyomino (and associated) literature, these objects are usually referred to as cells, sites and bonds, respectively. Just as we constructed polyominoes from cells, we can construct all sorts of connected objects on the grid from combinations of cells, sites and bonds. Let us first consider objects constructed from just one of these three things.

Definition 2
In the same way that a polyomino is a connected union of cells, we define:

• a site animal is a connected union of sites, and
• a bond animal is a connected union of bonds.

Site animals and polyominoes are closely related objects -- if we replace each cell of a polyomino with a site at its centre, a polyomino is replaced with a site animal on the dual lattice¹⁵ (see figure ). Consequently if a family of polyominoes can be enumerated according to their area, then the corresponding family of site animals is also solved.

Figure 10: Polyominoes with square and hexagonal cells, and the corresponding site animals on the dual lattices.

In this section we describe some of the most commonly studied site animals, bond animals and polyominoes; self-avoiding polygons or SAPs (see [32] for example) take a special place in this classification, since they are defined both as bond animals and polyominoes (see figure 11). If we consider the perimeter of the polygon then:

Definition 3
A self-avoiding polygon is a bond animal for which every vertex visited by the animal is of degree 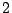$2$. Alternatively it is the embedding of a simple closed loop into the square grid.

On the other hand, if we consider the interior of the polygon then:

Definition 4
A self-avoiding polygon is a polyomino with no holes; all cells that are not a part of the polygon, must be connected to 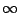$\infty$.

Figure: Polygons: If we consider only the perimeter, then a polygon is a bond animal. If we consider the interior (area), then a polygon is a polyomino. If we consider both area and perimeter, then a polygon is somehow a bond-cell animal.

Polyominoes, site-animals, bond-animals and self-avoiding polygons remain unsolved in two dimensions and higher; the best solutions remain either brute-force methods or algorithms that are exponentially faster than brute-force, but still require exponential time. It is not certain that any of these models do have a ``nice'' solution; no-one has proved that 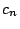$c_n$ can be computed in polynomial time. Imposing topological restrictions on these models allows us to make some progress; if we simplify the possible animal and polyomino ``topologies'' then we can find solutions. Indeed all solved models have strict topological restrictions; with the exception of only two¹⁶, all are either directed or convex or both (see below and chapter 2).

Below we give a taxonomy of these models, both solved and unsolved, which we have divided into three parts:

• site animals and polyominoes -- enumerated according to area (number of sites or cells),
• bond animals -- enumerated according to the number of bonds,
• polygon models -- enumerated according to perimeter (number of bonds) and area (number of cells).

Since polygon models can be considered both as polyominoes and bond-animals, it makes sense to describe them separately. Further since there are a large number of polygon models to describe we have given the majority of their definitions in chapter 2. One could construct more complicated objects, however we do not explore this possibility in this thesis.

By far the majority of polyomino and animal results are for the square lattice, and it should be assumed (unless stated otherwise) that the definitions and results described below are for the square lattice.